题目内容

19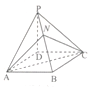．如图，四棱锥P-ABCD的底面ABCD为平行四边形，NB=2PN，则三棱锥N-PAC与三棱锥D-PAC的体积之比为（　　）
A．1：2B．1：3C．1：4D．1：6

分析 由题意得到N与D到平面PAC的距离的关系，结合棱锥体积公式得答案．

解答 解：如图，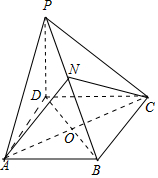

设平面PAC的面积为S，
∵底面ABCD为平行四边形，∴D到平面PAC的距离等于B到平面PAC的距离，
又NB=2PN，∴N到平面PAC的距离等于B到平面PAC距离的$\frac{1}{3}$．
设N到平面PAC的距离为h，则D到平面PAC的距离为3h．
∴${V}_{N-PAC}=\frac{1}{3}Sh$，${V}_{D-PAC}=\frac{1}{3}S•3h=Sh$．
∴三棱锥N-PAC与三棱锥D-PAC的体积之比为1：3．
故选：B．

点评 本题考查三棱锥体积的求法，考查空间想象能力和思维能力，属中档题．

练习册系列答案
相关题目
9．运行如图所示的程序框图，则输出的结果S=（　　）
A．1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{99}$B．$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{99}$C．1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{101}$D．$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{101}$
10．已知，0＜β＜α＜$\frac{π}{4}$，cos（α-β）=$\frac{12}{13}$，且sin（α+β）=$\frac{4}{5}$，则sin2α的值为$\frac{63}{65}$．
7．在直角梯形ABCD中，∠A=90°，AD∥BC，BC=2AD，△ABD面积为1，若$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{EC}$，BE⊥CD，则$\overrightarrow{DA}$•$\overrightarrow{DC}$=$-\sqrt{2}$．
14．已知函数f（x）=|x-a|，若不等式f（x）≤3的解集为{|x|-1≤x≤5}．
（Ⅰ）求实数a的值：
（Ⅱ）若不等式f（3x）+f（x+3）≥m对一切实数x恒成立，求实数m的取值范围．
4．已知函数f（x）=（t+1）lnx+tx2+3t，t∈R．
（1）若t=0，求证：当x≥0时，f（x+1）≥x-$\frac{1}{2}$x2；
（2）若f（x）≥4x对任意x∈[1，+∞）恒成立，求t的取值范围．
11．已知数列{an}是各项均不为零的等差数列，Sn为其前n项和，且${a_n}=\sqrt{{S_{2n-1}}}$（n∈N*）．若不等式$\frac{{λ{{（-1）}^n}}}{a_n}≤\frac{{n+2{{（-1）}^{n+1}}}}{n}$对任意n∈N*恒成立，则实数λ的取值范围是[-3，0]．
8．已知正方体的表面积为24，则该正方体的体积为（　　）
A．8B．27C．64D．125
9．执行如图的程序框图，则输出的S值为（　　）
A．33B．215C．343D．1025

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网