题目内容
3.已知两条不同直线m、l,两个不同平面α、β,下列命题正确的是( )| A. | 若l∥α,则l平行于α内的所有直线 | B. | 若m?α,l?β且l⊥m,则α⊥β | ||
| C. | 若l?β,l⊥α,则α⊥β | D. | 若m?α,l?β且α∥β,则m∥l |
分析 由线面平行的性质定理可知A错误;若m?α,l?β且l⊥m,则α、β位置关系不确定;根据平面与平面垂直的判定定理可得结论;由平面与平面平行的性质定理可得结论.
解答 解:由线面平行的性质定理:若l∥α,l⊆β,α∩β=m,则l∥m可知,A错误;
若m?α,l?β且l⊥m,则α、β位置关系不确定,B错误;
根据平面与平面垂直的判定定理,可知C正确;
由平面与平面平行的性质定理,可知D不正确.
故选C.
点评 本题主要考查了直线与平面,平面与平面的位置关系及判定定理、性质定理的综合应用,属于知识的综合应用.

练习册系列答案
相关题目
13.设函数f(x)是定义在R上的奇函数,则下列结论中一定正确的是( )
| A. | 函数f(x)+x2是奇函数 | B. | 函数f(x)+|x|是偶函数 | ||
| C. | 函数x2f(x)是奇函数 | D. | 函数|x|f(x)是偶函数 |
11.若双曲线$\frac{x^2}{3}-{y^2}=1$的左焦点在抛物线y2=2px的准线上,则p的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | $4\sqrt{2}$ |
18.某单位生产A、B两种产品,需要资金和场地,生产每吨A种产品和生产每吨B种产品所需资金和场地的数据如表所示:
现有资金12万元,场地400平方米,生产每吨A种产品可获利润3万元;生产每吨B种产品可获利润2万元,分别用x,y表示计划生产A、B两种产品的吨数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问A、B两种产品应各生产多少吨,才能产生最大的利润?并求出此最大利润.
| 资源 产品 | 资金(万元) | 场地(平方米) |
| A | 2 | 100 |
| B | 35 | 50 |
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问A、B两种产品应各生产多少吨,才能产生最大的利润?并求出此最大利润.
8.已知点A($\sqrt{3}$,0)和P($\sqrt{3}$,t)(t∈R).若曲线x=$\sqrt{3-{y}^{2}}$上存在点B使∠APB=60°,则t的取值范围是( )
| A. | (0,1+$\sqrt{3}$] | B. | [0,1+$\sqrt{3}$] | C. | [-1-$\sqrt{3}$,1+$\sqrt{3}$] | D. | [-1-$\sqrt{3}$,0)∪(0,1+$\sqrt{3}$] |
5.已知x、y满足约束条件$\left\{\begin{array}{l}{x-y≥1}\\{2x-y+1≤0}\end{array}\right.$,且目标函数z=mx-ny(m>0,n<0)的最大值为-6,则$\frac{n}{m-1}$的取值范围是( )
| A. | [-2,0]∪[$\frac{1}{2}$,+∞) | B. | [2,+∞) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,0)∪[$\frac{1}{2}$,+∞) |
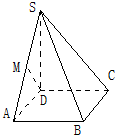 如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SD=1,SB=$\sqrt{3}$.
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SD=1,SB=$\sqrt{3}$.