题目内容
5.已知Sn是数列{an}的前n项和,a1=2,Sn+1=$\frac{1}{2}$Sn+2(n∈N*),则Sn的取值范围是( )| A. | (2,4] | B. | [2,4) | C. | [2,4] | D. | [2,+∞) |
分析 a1=2,Sn+1=$\frac{1}{2}$Sn+2(n∈N*),变形为Sn+1-4=$\frac{1}{2}$(Sn-4),利用等比数列的通项公式可得Sn,再利用数列的单调性与指数函数的单调性即可得出.
解答 解:∵a1=2,Sn+1=$\frac{1}{2}$Sn+2(n∈N*),
∴Sn+1-4=$\frac{1}{2}$(Sn-4),
∴数列{Sn-4}是等比数列,首项为-2,公比为$\frac{1}{2}$,
∴Sn-4=$-2×(\frac{1}{2})^{n-1}$,
∴Sn=4$-2×(\frac{1}{2})^{n-1}$=4-$(\frac{1}{2})^{n-2}$∈[2,4),
故选:B.
点评 本题考查了等比数列的通项公式、数列的单调性与指数函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.已知$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(1,λ),且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ为锐角,则实数λ的取值范围是( )
| A. | (-∞,-2)∪(-2,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,+∞) | C. | (-2,$\frac{2}{3}$)∪($\frac{2}{3}$,+∞) | D. | (-∞,$\frac{1}{2}$) |
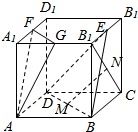 如图,在正方体ABCD-A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,求证:
如图,在正方体ABCD-A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,求证: