题目内容
16.设函数f(x)=1+$\frac{{x}^{\frac{1}{3}}+x}{{x}^{\frac{2}{3}}+{x}^{2}}$(x∈[-b,-a]∪[a,b],其中a<b)的最大值为M,最小值为m,则M+m=2.分析 设g(x)=$\frac{{x}^{\frac{1}{3}}+x}{{x}^{\frac{2}{3}}+{x}^{2}}$(x∈[-b,-a]∪[a,b],其中a<b),则g(x)是奇函数,可得g(x)max+g(x)min=0,根据f(x)=1+$\frac{{x}^{\frac{1}{3}}+x}{{x}^{\frac{2}{3}}+{x}^{2}}$(x∈[-b,-a]∪[a,b],其中a<b)的最大值为M,最小值为m,可得M-1+m-1=0,即可求出M+m.
解答 解:设g(x)=$\frac{{x}^{\frac{1}{3}}+x}{{x}^{\frac{2}{3}}+{x}^{2}}$(x∈[-b,-a]∪[a,b],其中a<b),则g(x)是奇函数,
∴g(x)max+g(x)min=0,
∵f(x)=1+$\frac{{x}^{\frac{1}{3}}+x}{{x}^{\frac{2}{3}}+{x}^{2}}$(x∈[-b,-a]∪[a,b],其中a<b)的最大值为M,最小值为m,
∴M-1+m-1=0
∴M-m=2.
故答案为:2.
点评 本题考查函数的奇偶性与最值,考查学生的计算能力,确定函数的奇偶性是关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
4.函数y=$\sqrt{{x}^{2}-2x-3}$的定义域为( )
| A. | [-1,3] | B. | (-∞,-1)∪(3,+∞) | C. | (-1,3) | D. | (-∞,-1]∪[3,+∞) |
11.设n=${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$3cosxdx,则二项式(2x+$\frac{1}{\root{3}{x}}$)n的展开式中x2项的系数为( )
| A. | 80 | B. | 90 | C. | 120 | D. | 160 |
5.已知Sn是数列{an}的前n项和,a1=2,Sn+1=$\frac{1}{2}$Sn+2(n∈N*),则Sn的取值范围是( )
| A. | (2,4] | B. | [2,4) | C. | [2,4] | D. | [2,+∞) |
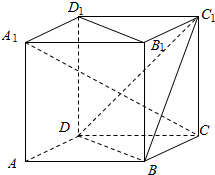 如图,ABCD-A1B1C1D1是棱长为1正方体.
如图,ABCD-A1B1C1D1是棱长为1正方体.