题目内容
曲线y=cosx,x∈[
,
]与坐标轴所围成的面积为 .
| π |
| 2 |
| 3π |
| 2 |
考点:余弦函数的图象
专题:计算题,函数的性质及应用
分析:本题利用直接法求解,根据三角函数的对称性知,曲线y=cosx与直线x=
、x=
、y=0所围成的平面区域的面积S为:曲线y=cosx与直线x=
,x=π所围成的平面区域的面积的二倍,最后结合定积分计算面积即可.
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
解答:
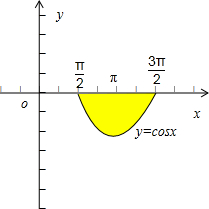 解:根据对称性,得:
解:根据对称性,得:
曲线y=cosx与直线x=
、x=
、y=0所围成的平面区域的面积S为:
曲线y=cosx与直线x=
,x=π所围成的平面区域的面积的二倍,
∴S=-2
cosxdx=-2sinx|
=-2(sinπ-sin
)=2.
故曲线y=cosx与直线x=
、x=
、y=0所围成的面积为2.
故答案为:2.
 解:根据对称性,得:
解:根据对称性,得:曲线y=cosx与直线x=
| π |
| 2 |
| 3π |
| 2 |
曲线y=cosx与直线x=
| π |
| 2 |
∴S=-2
| ∫ | π
|
π
|
| π |
| 2 |
故曲线y=cosx与直线x=
| π |
| 2 |
| 3π |
| 2 |
故答案为:2.
点评:本小题主要考查定积分应用、三角函数的图象等基础知识,考查考查数形结合思想,属于中档题.

练习册系列答案
相关题目
巳知角α的终边与单位圆交于点(-
,
),则sin2α的值为( )
2
| ||
| 5 |
| ||
| 5 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知
=(-1,2),
=(2,λ),且
与
的夹角为钝角,则实数λ的取值范围是( )
| a |
| b |
| a |
| b |
| A、(-∞,1) |
| B、(0,1) |
| C、(1,∞) |
| D、(-∞,-4)∪(-4,1) |
(普通文科做)已知i为虚数单位,则i2012的值为( )
| A、i | B、-i | C、-1 | D、1 |