题目内容
5.已知实数x,y满足$\left\{\begin{array}{l}{2x-y≥0}\\{x+2y-5≤0}\\{y≥1}\end{array}\right.$,则z=$\frac{{x}^{2}+{y}^{2}}{xy}$大值为$\frac{10}{3}$.分析 画出可行域,求出$\frac{y}{x}$的范围,利用目标函数求解最大值即可.
解答 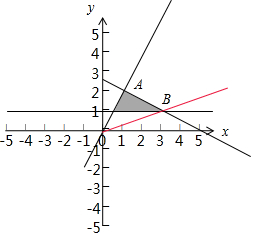 解:实数x,y满足$\left\{\begin{array}{l}{2x-y≥0}\\{x+2y-5≤0}\\{y≥1}\end{array}\right.$的可行域如图:
解:实数x,y满足$\left\{\begin{array}{l}{2x-y≥0}\\{x+2y-5≤0}\\{y≥1}\end{array}\right.$的可行域如图:
,$z=\frac{{{x^2}+{y^2}}}{xy}=\frac{x}{y}+\frac{y}{x}$,令$t=\frac{y}{x}$,作出可行域知$t=\frac{y}{x}$的取值范围[kOB,kOA],易知:A(1,2),B(3,1)
可得$t∈[\frac{1}{3},2]$,于是$z=\frac{{{x^2}+{y^2}}}{xy}=t+\frac{1}{t}$,
t∈(1,2],函数是增函数,t∈($\frac{1}{3},1$)函数是减函数,t=$\frac{1}{3}$时,z取得最大值为$\frac{10}{3}$.
故答案为:$\frac{10}{3}$.
点评 本题考查线性规划的简单应用,判断目标函数的几何意义,函数的最值是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
16.已知集合A={x|(5x+1)(x-4)<0},B={x|x<2},则A∩B等于( )
| A. | (-∞,4) | B. | $({-\frac{1}{5},2})$ | C. | (2,4) | D. | $({-∞,-\frac{1}{5}})∪({2,4})$ |
20.已知函数f(x)=sin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的零点构成一个公差为$\frac{π}{2}$的等差数列,$f(0)=-\frac{{\sqrt{3}}}{2}$,则f(x)的一个单调递增区间是( )
| A. | $(-\frac{5π}{12},\frac{π}{12})$ | B. | $(-\frac{π}{6},\frac{π}{3})$ | C. | $(-\frac{π}{12},\frac{5π}{12})$ | D. | $(\frac{π}{12},\frac{7π}{12})$ |
10.已知函数f(x)=Asin(ωx+φ),x∈R(其中$A>0,ω>0,0<Φ<\frac{π}{2}$)的图象与x轴的交点中,相邻的两个交点之间的距离为$\frac{π}{2}$,且图象上的一个最低点为$M(\frac{2π}{3},-2)$,则f(x)的解析式为( )
| A. | $f(x)=2sin(2x+\frac{π}{6})$ | B. | $f(x)=2cos(2x+\frac{π}{6})$ | C. | $f(x)=sin(2x+\frac{π}{3})$ | D. | $f(x)=cos(2x+\frac{π}{3})$ |