题目内容
14．
如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（6，4），则$\underset{lim}{△x→0}$$\frac{f（1+△x）-f（1）}{△x}$=-2（用数字作答）．
分析 由导数和切线斜率的关系，求极限可得．
解答 解：由题意可得AB的斜率k=$\frac{0-4}{2-0}$=-2，
∴直线AB的方程为y-0=-2（x-2），
∴当0≤x≤2时，f（x）=y=-2x+4，
∴$\underset{lim}{△x→0}$$\frac{f（1+△x）-f（1）}{△x}$=$\underset{lim}{△x→0}$$\frac{-2（1+△x）+4+2×1-4}{△x}$=-2
故答案为：-2
点评 本题考查极限的运算，涉及导数的定义，属基础题．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
9．下列函数为偶函数的是（ ）
| A． | f（x）=x | B． | f（x）=x3 | C． | f（x）=x2，x∈（-5，5] | D． | f（x）=4 |
19．
某厂通过技术改造降低了产品A对重要原材料G的消耗，如表提供了该厂技术改造后生产产品A的过程记录的产量x（吨）与原材料G相应的消耗量y（吨）的几组对照数据：
（1）请在图a中画出如表数据的散点图；
（2）请根据如表提供的数据，用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（3）试根据（2）求出的线性回归方程，预测生产50吨产品A需要消耗原材料G多少吨？参考公式：最小二乘法求线性回归方程
系数公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
某厂通过技术改造降低了产品A对重要原材料G的消耗，如表提供了该厂技术改造后生产产品A的过程记录的产量x（吨）与原材料G相应的消耗量y（吨）的几组对照数据：| x | 3 | 4 | 5 | 6 |
| y | 1.6 | 2.2 | 3.0 | 3.4 |
（2）请根据如表提供的数据，用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（3）试根据（2）求出的线性回归方程，预测生产50吨产品A需要消耗原材料G多少吨？参考公式：最小二乘法求线性回归方程
系数公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
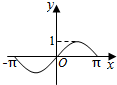
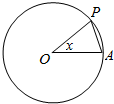如图，圆O的半径为1，A是圆上的定点，P是圆上的动点，角x的始边为射线OA，终边为射线OP，将△POA的面积表示为x的函数f（x），则y=f（x）在[-π，π]上的图象大致为（ ）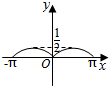
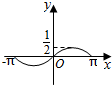
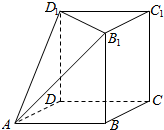如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分．