题目内容
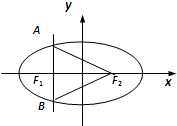 已知点F1、F2分别是椭圆
已知点F1、F2分别是椭圆| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先求出 AF1 的长,直角三角形AF1;F2 中,由边角关系得tan30°=
=
=
=,解方程能求出离心率的值.
| ||
| 3 |
| |AF1| |
| |F1F2| |
| ||
| 2c |
解答:
解:∵点F1、F2分别是椭圆
+
=1的左、右焦点,
过F1且垂直于x轴的直线与椭圆交于A、B两点,
把x=-c代入椭圆的方程可得y=
,
∴AF1 =
,
∵△ABF2为正三角形,
∴由tan30°=
=
=
=
=
,
∴3e2+2
e-3=0,解得 e=-
(舍去),或e=
.
故答案为:
.
| x2 |
| a2 |
| y2 |
| b2 |
过F1且垂直于x轴的直线与椭圆交于A、B两点,
把x=-c代入椭圆的方程可得y=
| b2 |
| a |
∴AF1 =
| b2 |
| a |
∵△ABF2为正三角形,
∴由tan30°=
| ||
| 3 |
| |AF1| |
| |F1F2| |
| ||
| 2c |
| a2-c2 |
| 2ac |
| 1-e2 |
| 2e |
∴3e2+2
| 3 |
| ||
| 3 |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查椭圆的简单性质,直角三角形中的边角关系,解方程求离心率的大小,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
以下判断正确的是( )
| A、函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件 |
| B、命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” |
| C、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
| D、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
已知集合A={x|-2≤x≤2},B={x|0<x<1},则有( )
| A、A>B | B、A?B |
| C、B?A | D、A⊆B |
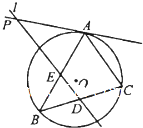 如图,△ABC内接于⊙O,过BC中点D作平行于AC的直线l,l交AB于E,交⊙O在A点处的切线于点P,若PE=6,ED=3,则AE的长为
如图,△ABC内接于⊙O,过BC中点D作平行于AC的直线l,l交AB于E,交⊙O在A点处的切线于点P,若PE=6,ED=3,则AE的长为 如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若CD=
如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若CD=