题目内容
“a=2”是“关于x的不等式|x+1|+|x+2|<a的解集非空”的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分又不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据绝对值的性质,利用充分条件和必要条件的定义进行判断.
解答:
解:∵|x+1|+|x+2|≥1,
∴要使关于x的不等式|x+1|+|x+2|<a的解集非空,
则a>1,
∴“a=2”是“关于x的不等式|x+1|+|x+2|<a的解集非空”的充分不必要条件.
故选:C.
∴要使关于x的不等式|x+1|+|x+2|<a的解集非空,
则a>1,
∴“a=2”是“关于x的不等式|x+1|+|x+2|<a的解集非空”的充分不必要条件.
故选:C.
点评:本题主要考查充分条件和必要条件的判断,根据绝对值的意义是解决本题本题的关键.

练习册系列答案
相关题目
以下判断正确的是( )
| A、函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件 |
| B、命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” |
| C、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
| D、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
已知集合A={x|-2≤x≤2},B={x|0<x<1},则有( )
| A、A>B | B、A?B |
| C、B?A | D、A⊆B |
已知偶函数f(x)在[0,+∞)上单调递减,则f(1)和f(-10)的大小关系为( )
| A、f(1)>f(-10) |
| B、f(1)<f(-10) |
| C、f(1)=f(-10) |
| D、f(1)和f(-10)关系不定 |
把6个人平均分成两组,再从各组中分别选出正组长1名和副组长1名,则不同的选法种数是( )
| A、720 | B、360 |
| C、120 | D、60 |
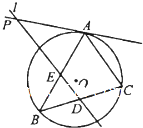 如图,△ABC内接于⊙O,过BC中点D作平行于AC的直线l,l交AB于E,交⊙O在A点处的切线于点P,若PE=6,ED=3,则AE的长为
如图,△ABC内接于⊙O,过BC中点D作平行于AC的直线l,l交AB于E,交⊙O在A点处的切线于点P,若PE=6,ED=3,则AE的长为 如图是一个从A→B的”闯关”游戏.规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于2n,则闯关成功.
如图是一个从A→B的”闯关”游戏.规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于2n,则闯关成功.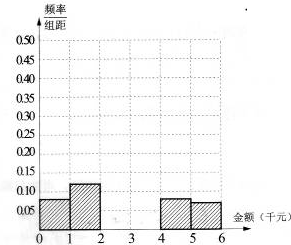 某网络营销部门随机抽查了某市200名网友在2013年11月11日的网购金额,所得数据如下表:
某网络营销部门随机抽查了某市200名网友在2013年11月11日的网购金额,所得数据如下表: