题目内容
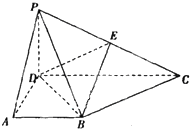 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2.(Ⅰ)求证:BC⊥平面PBD;
(Ⅱ)问侧棱PC上是否存在异于端点的一点E,使得二面角E-BD-P的余弦值为
| ||
| 3 |
考点:直线与平面垂直的判定,二面角的平面角及求法
专题:证明题,空间位置关系与距离
分析:(Ⅰ)以D为原点建立空间直角坐标系D-xyz,根据线面垂直的判定定理即可证明BC⊥平面PBD;
(Ⅱ)由
=(0,2,-1),又
=λ
且λ∈(0,1),设E(x0,y0,z0),可得
=(0,2λ,1-λ),设平面EBD的法向量为
=(a,b,c),令a=-1,则可得平面EBD的一个法向量为
=(-1,1,
),而平面PDB的法向量即为
=(-1,1,0),可得
=|
|,即可解得λ的值,从而得解.
(Ⅱ)由
| PC |
| PE |
| PC |
| DE |
| n |
| n |
| 2λ |
| λ-1 |
| BC |
| ||
| 3 |
| ||||
|
|
解答:
 解:(Ⅰ)平面PCD⊥底面ABCD,PD⊥CD,所以PD⊥平面ABCD,
解:(Ⅰ)平面PCD⊥底面ABCD,PD⊥CD,所以PD⊥平面ABCD,
所以PD⊥AD.如图,以D为原点建立空间直角坐标系D-xyz.
则A(1,0,0),B(1,1,0),C(0,2,0),P(0,0,1),
=(1,1,0).
=(-1,1,0)
所以
•
=0,所以BC⊥BD,
又由PD⊥平面ABCD,可得PD⊥BC,又PD∩DB=D,
所以BC⊥平面PBD.
(Ⅱ)因为
=(0,2,-1),又
=λ
且λ∈(0,1),设E(x0,y0,z0),
则(x0,y0,z0-1)=(0,2λ,-λ),
所以,E(0,2λ,1-λ),即
=(0,2λ,1-λ),.…(6分)
设平面EBD的法向量为
=(a,b,c),
因为
=(1,1,0),由
•
=0,
•
=0,
得
,
令a=-1,则可得平面EBD的一个法向量为
=(-1,1,
)…(9分)
而平面PDB的法向量即为
=(-1,1,0)…(10分)
所以,
=|
|=
,
解得λ=
或λ=-1,…(11分)
又由题意知λ∈(0,1),故λ=
,即点E在靠近点P的三等分处.…(12分)
 解:(Ⅰ)平面PCD⊥底面ABCD,PD⊥CD,所以PD⊥平面ABCD,
解:(Ⅰ)平面PCD⊥底面ABCD,PD⊥CD,所以PD⊥平面ABCD,所以PD⊥AD.如图,以D为原点建立空间直角坐标系D-xyz.
则A(1,0,0),B(1,1,0),C(0,2,0),P(0,0,1),
| DB |
| BC |
所以
| DB |
| BC |
又由PD⊥平面ABCD,可得PD⊥BC,又PD∩DB=D,
所以BC⊥平面PBD.
(Ⅱ)因为
| PC |
| PE |
| PC |
则(x0,y0,z0-1)=(0,2λ,-λ),
所以,E(0,2λ,1-λ),即
| DE |
设平面EBD的法向量为
| n |
因为
| DB |
| n |
| DB |
| n |
| DE |
得
|
令a=-1,则可得平面EBD的一个法向量为
| n |
| 2λ |
| λ-1 |
而平面PDB的法向量即为
| BC |
所以,
| ||
| 3 |
| ||||
|
|
| 2 | ||||||
|
解得λ=
| 1 |
| 3 |
又由题意知λ∈(0,1),故λ=
| 1 |
| 3 |
点评:本题主要考查空间直线和平面,平行和垂直的判定,以及空间二面角的求解,要求熟练掌握相应的判定定理以及空间向量与二面角的关系,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在2,0,1,5这组数据中,随机取出三个不同的数,则数字2是取出的三个不同数的中位数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|