题目内容
12.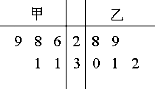 为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
④甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差;
其中根据茎叶图能得到的统计结论的标号为( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
分析 利用茎叶图分别求出甲、乙两地某月14时的气温的平均值和标准差,由此能求出结果.
解答 解:由茎叶图,得:
甲地该月14时的平均气温$\overline{{x}_{甲}}$=$\frac{1}{5}$(26+28+29+31+31)=29,
甲地该月14时的平均气温的标准差S甲=$\sqrt{\frac{1}{5}[(-3)^{2}+(-1)^{2}+{0}^{2}+{2}^{2}+{2}^{2}]}$=$\sqrt{3.6}$,
乙地该月14时的平均气温$\overline{{x}_{乙}}$=$\frac{1}{5}$(28+29+30+31+32)=30,
乙地该月14时的平均气温的标准差S乙=$\sqrt{\frac{1}{5}[(-2)^{2}+(-1)^{2}+{0}^{2}+{1}^{2}+{2}^{2}]}$=$\sqrt{2}$,
∴甲地该月14时的平均气温低于乙地该月14时的平均气温,
甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.
∴根据茎叶图能得到的统计结论的标号为①③.
故选:A.
点评 本题考查平均值、标准差的求法,是基础题,解题时要认真审题,注意茎叶图、平均值、标准差的合理运用.

练习册系列答案
相关题目
5.已知函数f(x)=alnx的导函数是f′(x)且f′(2)=2,则实数的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | 4 |
6.小明和小东两人比赛下象棋,小明不输的概率是$\frac{3}{4}$,小东输的概率是$\frac{1}{2}$,则两人和棋的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
4.已知|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=5,且$\overrightarrow{a}•\overrightarrow{b}$=12,则向量$\overrightarrow{a}$在向量$\overrightarrow{b}$上的投影为( )
| A. | $\frac{12}{5}$ | B. | 4 | C. | $-\frac{12}{5}$ | D. | -4 |
1.命题“若x+y=1,则xy≤1”的否命题是( )
| A. | 若x+y=1,则xy>1 | B. | 若x+y≠1,则xy≤1 | C. | 若x+y≠1,则xy>1 | D. | 若xy>1,则x+y≠1 |
2.已知直线l1:y=-1和直线l2:3x-4y+19=0,抛物线x2=4y上一动点P到直线l1和直线l2的距离之和最小值为( )
| A. | 3 | B. | 2 | C. | $\frac{24}{5}$ | D. | $\frac{5}{2}$ |