题目内容
下列命题中,真命题的是( )
| A、?0∈R,e x0≤0 |
| B、?x∈R,2x>x2 |
| C、a-b>0是a3-b3>0的充分不必要条件 |
| D、ab>1是a>1且b>1的必要不充分条件 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:分别根据命题的真假关系进行判断即可得到结论.
解答:
解:A.?x∈R,ex>0,∴A错误.
B.当x=2时,22=22=4,∴B错误.
C.∵函数y=x3,单调递增,∴a-b>0是a3-b3>0的充分必要条件,∴C错误.
D.当a=-2,b=-2时,满足ab>1,但a>1且b>1不成立,充分性不成立,
若a>1且b>1,则必有ab>1,即ab>1是a>1且b>1的必要不充分条件,正确,
故选:D.
B.当x=2时,22=22=4,∴B错误.
C.∵函数y=x3,单调递增,∴a-b>0是a3-b3>0的充分必要条件,∴C错误.
D.当a=-2,b=-2时,满足ab>1,但a>1且b>1不成立,充分性不成立,
若a>1且b>1,则必有ab>1,即ab>1是a>1且b>1的必要不充分条件,正确,
故选:D.
点评:本题主要考查了命题的真假判断,要求熟练掌握含有量词的命题的真假判断,以及充分条件和必要条件的定义.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
已知函数f(x)(x∈R)的图象上任一点(x0,y0)处切线的方程为:y-y0=(x0-2)( x0-1)(x-x0),那么函数f(x)的单调减区间是( )
| A、(1,2) |
| B、(-∞,1] |
| C、[2,+∞) |
| D、(-∞,-1) |
已知集合A={x|y=
},B={y|y=2x,x∈R},则A∩B=( )
| x-x2 |
| A、[0,1] |
| B、(0,1) |
| C、(0,1] |
| D、[0,1) |
函数f(x)=sinωx(ω>0)的图象在y轴右边的第一条对称轴的方程x=1,则ω=( )
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
在复平面内,复数
-i3对应的点位于( )
| 2 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知函数f(x)=ax2+bx+c(a,b,c∈R,a<0)对于一切实数x都有f(1-x)=f(1+x),而且f(-1)<0,f(0)>0,则有( )
| A、a+b+c<0 |
| B、c<2b |
| C、abc>0 |
| D、b<a+c |
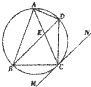 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.若AB=6,BC=4,则DE=
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.若AB=6,BC=4,则DE=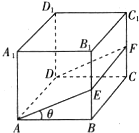 如图正方体ABCD-A1B1C1D1的棱长为1,点E在线段BB1和线段A1B1上移动,∠EAB=θ,θ∈(0,
如图正方体ABCD-A1B1C1D1的棱长为1,点E在线段BB1和线段A1B1上移动,∠EAB=θ,θ∈(0,