题目内容
13.某厂以x千克/小时的速度匀速生产某种产品(生产条件要求1≤x≤10),每一小时可获得的利润是$50(5x-\frac{3}{x}+1)$元.(1)要使生产该产品2小时获得的利润不低于1500元,求x的取值范围;
(2)要使生产480千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
分析 (1)利用已知条件列出不等式求解即可.
(2)利用二次函数的性质,通过配方求解函数的最值即可.
解答 解:(1)根据题意,
有$100(5x-\frac{3}{x}+1)≥1500$,
得5x2-14x-3≥0,得x≥3或$x≤-\frac{1}{5}$,
又1≤x≤10,得3≤x≤10.
(2)生产480千克该产品获得的利润为$u=24000(5+\frac{1}{x}-\frac{3}{x^2})$,1≤x≤10,
记$f(x)=-\frac{3}{x^2}+\frac{1}{x}+5$,1≤x≤10,
则$f(x)=-3{(\frac{1}{x}-\frac{1}{6})^2}+\frac{1}{12}+5$
当且仅当x=6时取得最大值$\frac{61}{12}$,
则获得的最大利润为$u=24000×\frac{61}{12}=122000$(元)
故该厂以6千克/小时的速度生产,可获得最大利润为122000元.
点评 本题考查函数的实际应用,二次函数的性质,考查计算能力.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
5. 如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )
如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )
 如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )
如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )| A. | i≤1009 | B. | i>1009 | C. | i≤1010 | D. | i>1010 |
18.命题“?x0∈(0,+∞),lnx0=2x0+1”的否定是( )
| A. | ?x0∈(0,+∞),lnx0≠2x0+1 | B. | ?x0∉(0,+∞),lnx0=2x0+1 | ||
| C. | ?x∈(0,+∞),lnx≠2x+1 | D. | ?x∉(0,+∞),lnx≠2x+1 |
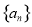 满足
满足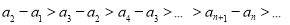 ,则称数列
,则称数列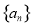 为“差递减”数列.若数列
为“差递减”数列.若数列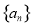 是“差递减”数列,且其通项
是“差递减”数列,且其通项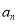 与其前
与其前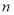 项和
项和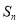 (
( )满足
)满足 (
(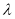 的取值范围是 .
的取值范围是 .