题目内容
求正弦函数y=sinx在0到
之间及
到
之间的平均变化率,并比较它们的大小.
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
考点:变化的快慢与变化率,导数的运算
专题:导数的概念及应用
分析:根据变化率的定义得出△x,△y,
.,
| △y |
| △x |
解答:
解:(1)∵正弦函数y=sinx,
∴△x=
,△y=
,
∴
=
=
,
(2)∵△x=
-
=
,△y=sin
-sin
=1-
,
∴
=
=
,
∵6-3
<3,
∴
<
∴△x=
| π |
| 6 |
| 1 |
| 2 |
∴
| △y |
| △x |
| ||
|
| 3 |
| π |
(2)∵△x=
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| ||
| 2 |
∴
| △y |
| △x |
1-
| ||||
|
6-3
| ||
| π |
∵6-3
| 3 |
∴
6-3
| ||
| π |
| 3 |
| π |
点评:本题考查了函数的变化率的运用求解,属于中档题,计算较麻烦,注意运用算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
| ∫ | 2 -2 |
| A、2e2-2 |
| B、2e2 |
| C、e2-e-2 |
| D、e2+e-2-2 |
若sin(π+θ)=-
,θ是第二象限角,sin(
+φ)=-
,φ是第三象限角,则cos(θ-φ)的值是( )
| 3 |
| 5 |
| π |
| 2 |
2
| ||
| 5 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
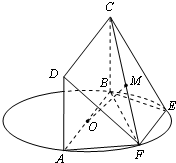 如图,AB为圆O的直径,四方形ABCD为正方形,点E,F在圆O上,AD⊥AF,AB=AF=2.
如图,AB为圆O的直径,四方形ABCD为正方形,点E,F在圆O上,AD⊥AF,AB=AF=2.