题目内容
已知函数f(x)=x2-2ax,x∈[1,3],求f(x)的最小值.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:函数f(x)=(x-a)2-a2 的图象的对称轴方程为x=a,分对称轴在区间[1,3]的左侧、中间、右侧三种情况,分别求得f(x)的最小值.
解答:
解:函数f(x)=x2-2ax=(x-a)2-a2 的图象的对称轴方程为x=a,当x∈[1,3]时,
当a<1时,函数的最小值为f(1)=1-2a;
当a∈[1,3]时,函数的最小值为f(a)=-a2;
当a>3时,函数的最小值为f(3)=9-6a.
当a<1时,函数的最小值为f(1)=1-2a;
当a∈[1,3]时,函数的最小值为f(a)=-a2;
当a>3时,函数的最小值为f(3)=9-6a.
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属基础题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
若复数
=a+bi(a,b∈R,i是虚数单位),则ab的值是( )
| 1+7i |
| i |
| A、3 | B、15 | C、-7 | D、-15 |
在平面直角坐标系中,若x,y满足约束条件
(k为常数),则能使z=x+y的最大值为10的k的值为( )
|
| A、10 | B、-10 |
| C、15 | D、-15 |
 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.求证:
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.求证: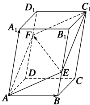 如图所示,在平行六面体ABCD-A1B1C1D1中,EF分别是B1B和D1D上的点,且BE=
如图所示,在平行六面体ABCD-A1B1C1D1中,EF分别是B1B和D1D上的点,且BE=