��Ŀ����
15������?n��N*��������{xn}����xn+1-xn��1������������Ϊ��K���С���������֪���У�1��m+1��m2�ǡ�K���С�����ʵ��m��ȡֵ��Χ��
�����Ƿ��������Ϊ-1�ĵȲ�����{an}Ϊ��K���С�������ǰn���Sn����${S_n}��\frac{1}{2}{n^2}-n��n��{N^*}��$�������ڣ����{an}��ͨ�ʽ���������ڣ���˵�����ɣ�
������֪�����Ϊ�������ĵȱ�����{an}�ǡ�K���С�������$\left\{{\frac{1}{2}{a_n}}\right\}$���ǡ�K���С�����${b_n}=\frac{{{a_{n+1}}}}{n+1}$�����ж�����{bn}�Ƿ�Ϊ��K���С�����˵�����ɣ�
���� ����������ã�m+1��-1��1��m2-��m+1����1������������ɵó���
��������ڵȲ�����{an}����Ҫ���蹫��Ϊd����d��1�������⣬��$-n+\frac{n��n-1��}{2}d��\frac{1}{2}{n^2}-n$��n��N*����������Ϊ��n-1��d��n����n�������۽�����ɵó���
����������{an}�Ĺ���Ϊq����${a_n}={a_1}{q^{n-1}}$��������ɵã�{an}��ÿһ���Ϊ����������an+1-an=anq-an=an��q-1����1��0���ɵ�a1��0����q��1����an+1-an=q��an-an-1����an-an-1���ɵ���{an-an-1}�У���a2-a1��Ϊ��С�ͬ������$\{\frac{1}{2}{a_n}-\frac{1}{2}{a_{n-1}}\}$�У���$\frac{1}{2}{a_2}-\frac{1}{2}{a_1}$��Ϊ��С������á�K���С����ɵ�a1=1��q=3��a1=2��q=2�������ó���
��� �⣺����������ã�m+1��-1��1����m2-��m+1����1����
��ٵ� m��1��
��ڵ� m��-1��m��2��
����m��2����ʵ��m��ȡֵ��Χ��m��2��
��������ڵȲ�����{an}����Ҫ���蹫��Ϊd����d��1��
�� a1=-1���� ${S_n}=-n+\frac{n��n-1��}{2}d$����
�����⣬��$-n+\frac{n��n-1��}{2}d��\frac{1}{2}{n^2}-n$��n��N*��������
����n-1��d��n��
�ٵ�n=1ʱ��d��R��
�ڵ�n��1ʱ��$d��\frac{n}{n-1}$��
��Ϊ$\frac{n}{n-1}=1+\frac{1}{n-1}��1$��
����d��1����d��1ì�ܣ�
�������ĵȲ�����{an}�����ڣ�
����������{an}�Ĺ���Ϊq����${a_n}={a_1}{q^{n-1}}$��
��Ϊ{an}��ÿһ���Ϊ����������an+1-an=anq-an=an��q-1����1��0��
����a1��0����q��1��
��Ϊan+1-an=q��an-an-1����an-an-1��
������{an-an-1}�У���a2-a1��Ϊ��С�
ͬ������$\{\frac{1}{2}{a_n}-\frac{1}{2}{a_{n-1}}\}$�У���$\frac{1}{2}{a_2}-\frac{1}{2}{a_1}$��Ϊ��С�
��{an}Ϊ��K���С���ֻ��a2-a1��1���� a1��q-1����1��
����Ϊ$\{\frac{1}{2}{a_n}\}$���ǡ�K���С����ҡ�$\frac{1}{2}{a_2}-\frac{1}{2}{a_1}$��Ϊ��С�����$\frac{1}{2}{a_2}-\frac{1}{2}{a_1}��1$���� a1��q-1����2��
������{an}��ÿһ���Ϊ���������ɵ� a1��q-1��=2��
����a1=1��q=3��a1=2��q=2��
�ٵ�a1=1��q=3ʱ��${a_n}={3^{n-1}}$����${b_n}=\frac{3^n}{n+1}$��
��${c_n}={b_{n+1}}-{b_n}��n��{N^*}��$����${c_n}=\frac{{{3^{n+1}}}}{n+2}-\frac{3^n}{n+1}={3^n}•\frac{2n+1}{��n+1����n+2��}$��
��${3^{n+1}}•\frac{2n+3}{��n+2����n+3��}-{3^n}•\frac{2n+1}{��n+1����n+2��}$=$\frac{3^n}{n+2}•\frac{{4{n^2}+8n+6}}{��n+1����n+3��}��0$��
����{cn}Ϊ�������У��� cn��cn-1��cn-2������c1��
����bn+1-bn��bn-bn-1��bn-1-bn-2������b2-b1��
��Ϊ${b_2}-{b_1}=3-\frac{3}{2}=\frac{3}{2}��1$��
���Զ������n��N*������bn+1-bn��1��
������{cn}Ϊ��K���С���
�ڵ�a1=2��q=2ʱ��${a_n}={2^n}$����${b_n}=\frac{{{2^{n+1}}}}{n+1}$����Ϊ${b_2}-{b_1}=\frac{2}{3}��1$��
��������{bn}���ǡ�K���С���
���ϣ���${a_n}={3^{n-1}}$ʱ������{bn}Ϊ��K���С���
��${a_n}={2^n}$ʱ������{bn}���ǡ�K���С���
���� ���⿼���˵Ȳ�������ȱ����е�ͨ�ʽ�����ʽ������ʽ�Ľⷨ���������۷�������������������������������������⣮

 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�| A�� | ��ֶ�����Ҫ���� | B�� | ��Ҫ����������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
| A�� | $\frac{��}{15}$ | B�� | $\frac{��}{12}$ | C�� | $\frac{��}{16}$ | D�� | $\frac{��}{18}$ |
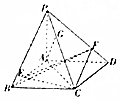 ��֪����P-ABCD�ĵ���ABCD��ƽ���ı��Σ�PA��ƽ��ABCD��PA=AB=AC=2��AD=2$\sqrt{2}$����E���߶�AB�Ͽ���B������ȷֵ㣬��F��G�ֱ����߶�PD��PC�ϣ�
��֪����P-ABCD�ĵ���ABCD��ƽ���ı��Σ�PA��ƽ��ABCD��PA=AB=AC=2��AD=2$\sqrt{2}$����E���߶�AB�Ͽ���B������ȷֵ㣬��F��G�ֱ����߶�PD��PC�ϣ�