题目内容
函数f(x)满足对定义域内的任意x,都有f(x+2)+f(x)<2f(x+1),则函数f(x)可以是( )
| A、f(x)=2x+1 |
| B、f(x)=x2-2x |
| C、f(x)=ex |
| D、f(x)=lnx |
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:将所给的不等式化为:“f(x+2)-f(x+1)<f(x+1)-f(x)”,得到不等式对应的函数含义,根据基本函数同为增函数时的增长情况,对答案项逐一进行判断即可.
解答:
解:由f(x+2)+f(x)<2f(x+1)得,
f(x+2)-f(x+1)<f(x+1)-f(x)①,
∵(x+2)-(x+1)=(x+1)-x,
∴①说明自变量变化相等时,当自变量越大时,对应函数值的变化量越来越小,
对于A、f(x)=2x+1是一次函数,且在R上直线递增,函数值的变化量是相等的,A错;
对于B、f(x)=x2-2x在定义域上不是单调函数,在(-∞,1)上递减,在(1,+∞)递增,B错;
对于C、f(x)=ex是增长速度最快-呈爆炸式增长的指数函数,当自变量越大时,
对应函数值的变化量越来越大,C错;
对于D、f(x)=lnx是增长越来越慢的对数函数,当自变量越大时,
对应函数值的变化量越来越小,D正确.
故选D.
f(x+2)-f(x+1)<f(x+1)-f(x)①,
∵(x+2)-(x+1)=(x+1)-x,
∴①说明自变量变化相等时,当自变量越大时,对应函数值的变化量越来越小,
对于A、f(x)=2x+1是一次函数,且在R上直线递增,函数值的变化量是相等的,A错;
对于B、f(x)=x2-2x在定义域上不是单调函数,在(-∞,1)上递减,在(1,+∞)递增,B错;
对于C、f(x)=ex是增长速度最快-呈爆炸式增长的指数函数,当自变量越大时,
对应函数值的变化量越来越大,C错;
对于D、f(x)=lnx是增长越来越慢的对数函数,当自变量越大时,
对应函数值的变化量越来越小,D正确.
故选D.
点评:本题考查了基本函数同为增函数时的增长速度的应用,此题的关键是将不等式进行转化,并能理解不等式所表达的函数意义,考查了分析问题、解决问题的能力.

练习册系列答案
相关题目
一个侧棱与底面垂直的四棱柱的正视图和俯视图如图所示,该四棱柱的体积为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的体积为( ) 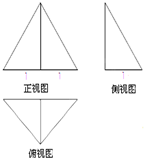

| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
阅读如图所示的算法框图,运行相应的程序,输出的结果是( )


| A、-1 | B、2 | C、3 | D、4 |
一物体的运动方程为s=
+2t(t>1),其中s的单位是米,t的单位是秒,那么物体在2秒末的瞬时速度是( )
| 1 |
| t |
A、
| ||
B、
| ||
C、
| ||
D、
|