题目内容

双曲线3x2-4y2=-12的焦点为F1、F2，则（　　）
A、F1（5，0），F2（-5），0
B、F1（
7
，0），F2（-
7
，0）
C、F1（0，
7
），F2（0，-
7
）
D、F1（1，0），F2（-1，0）
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：将双曲线方程化为标准方程，求出a，b，c，即可得到焦点坐标．
解答： 解：双曲线3x2-4y2=-12即为
y2
3
-
x2
4
=1，
则a=
3
，b=2，c=
3+4
=
7
．
则有双曲线的焦点为（0，-
7
），（0，
7
）．
故选：C．
点评：本题考查双曲线的方程和性质，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知Sn是等差数列{an}（n∈N*）的前n项和，且S6＞S7＞S5，有下列四个命题：①d＜0；②S11＞0；③S12＜0；④数列{Sn}中的最大项为S11，其中正确命题序号是（　　）
A、②③B、①②C、①③D、①④
已知椭圆
x2
a
2
1
+
y2
b
2
1
=1（a1＞b1＞0）的离心率为
2
2
，双曲线
x2
a
2
2
-
y2
b
2
2
=1（a2＞0，b2＞0）与椭圆有相同的焦点F1，F2，M是两曲线的一个公共点，若∠F1MF2=60°，则双曲线的渐进线方程为（　　）
A、y=±
2
2
x
B、y=±x
C、y=±
2
x
D、y=±
3
x
已知函数f（x）=
2-x
x
，x≥1
2x-1，x＜1
，g（x）=x2-2x，若关于x的方程f[g（x）]=k有四个不相等的实根，则实数k∈
 
．
直线l过圆x2+y2-2x+4y-4=0的圆心，且在y轴上的截距等于圆的半径，则直线l的方程为（　　）
A、5x+y-3=0
B、5x-y-3=0
C、4x+y-3=0
D、3x+2y-6=0
已知直线l：2x+y+4=0与圆C：x2+y2+2x-4y+1=0相交于A，B两点，求：
（1）线段AB的长；
（2）以AB为直径的圆M的标准方程．
已知A、B、C为△ABC的三个内角，且向量
m
=（1，cos
C
2
）与
n
=（
3
sin
C
2
+cos
C
2
，
3
2
）共线．求角C的大小．
满足tanA＞-1的三角形内角A的取值范围是（　　）
A、（0，
3π
4
）
B、（0，
π
2
）∪（
π
2
，
3π
4
）
C、（
3π
4
，π）
D、（0，
π
2
）∪（
3π
4
，π）
一个几何体的三视图如图所示，其中正视图是一个正三角形，则该几何体的体积为（　　）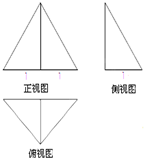 
A、1
B、
3
3
C、
3
D、
2
3
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网