题目内容
已知函数f(x)=
+lnx;
(1)当a=1时,若直线y=b与函数y=f(x)的图象在[
,2]上有两个不同交点,求实数b的取值范围;
(2)若函数f(x)在[1,+∞)上为增函数,求正实数a的取值范围;
(3)求证:对大于1的任意正整数n,lnn>
+
+
+…+
.
| 1-x |
| ax |
(1)当a=1时,若直线y=b与函数y=f(x)的图象在[
| 1 |
| 2 |
(2)若函数f(x)在[1,+∞)上为增函数,求正实数a的取值范围;
(3)求证:对大于1的任意正整数n,lnn>
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:计算题,证明题,导数的综合应用,不等式
分析:(1)a=1时,f(x)=
+lnx,x>0,fˊ(x)=
,由导数的正负确定函数的单调性,从而求实数b的取值范围;
(2)函数f(x)在[1,+∞)上为增函数可化为f′(x)=
≥0对x∈[1,+∞)恒成立;从而求a;
(3)由f(x)=
+lnx在[1,+∞)上为增函数可证明ln
>1-
=
,从而证明不等式.
| 1-x |
| x |
| x-1 |
| x2 |
(2)函数f(x)在[1,+∞)上为增函数可化为f′(x)=
| ax-1 |
| ax2 |
(3)由f(x)=
| 1-x |
| x |
| n |
| n-1 |
| 1 | ||
|
| 1 |
| n |
解答:
解:(1)a=1时,f(x)=
+lnx,x>0,
fˊ(x)=
,令fˊ(x)=0得x=1;
当x变化时,f(x),f′(x)的变化情况如下表:
∵1-ln2-(ln2-
)=
-2ln2=lne
-ln4>0,
∴b的取值范围为(0,ln2-
];
(2)∵f(x)=
+lnx,∴f′(x)=
(a>0);
∵函数f(x)在[1,+∞)上为增函数,
∴f′(x)=
≥0对x∈[1,+∞)恒成立;
既ax-1≥0对x∈[1,+∞)恒成立,
即a≥
对x∈[1,+∞)恒成立;
∴a≥1;
(3)证明:当a=1时,f(x)=
+lnx,x>0,
fˊ(x)=
,
故f(x)在[1,+∞)上为增函数.
∴f(x)≥f(1)=0,
∴
-1+lnx≥0,
∴lnx≥1-
,
当n>1时,则
>1,
∴ln
>1-
=
;
∴n>1时,lnn=ln
+ln
+…+ln
>
+
+
+…+
.
| 1-x |
| x |
fˊ(x)=
| x-1 |
| x2 |
当x变化时,f(x),f′(x)的变化情况如下表:
| x |
| (
| 1 | (1,2) | 2 | ||||
| fˊ(x) | - | 0 | + | ||||||
| f(x) | 1-ln2 | 单调递减 | 0 | 单调递增 | ln2-
|
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴b的取值范围为(0,ln2-
| 1 |
| 2 |
(2)∵f(x)=
| 1-x |
| ax |
| ax-1 |
| ax2 |
∵函数f(x)在[1,+∞)上为增函数,
∴f′(x)=
| ax-1 |
| ax2 |
既ax-1≥0对x∈[1,+∞)恒成立,
即a≥
| 1 |
| x |
∴a≥1;
(3)证明:当a=1时,f(x)=
| 1-x |
| x |
fˊ(x)=
| x-1 |
| x2 |
故f(x)在[1,+∞)上为增函数.
∴f(x)≥f(1)=0,
∴
| 1 |
| x |
∴lnx≥1-
| 1 |
| x |
当n>1时,则
| n |
| n-1 |
∴ln
| n |
| n-1 |
| 1 | ||
|
| 1 |
| n |
∴n>1时,lnn=ln
| 2 |
| 1 |
| 3 |
| 2 |
| n |
| n-1 |
>
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
点评:本题考查了导数的综合应用,同时考查了不等式的证明与恒成立问题,属于难题.

练习册系列答案
相关题目
若关于x的不等式|x-1|<ax的解集中恰好有两个整数,则a的取值范围是( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
| D、(-1,0) |
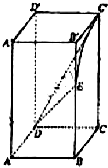 如图,四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面ABCD,AB=3
如图,四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面ABCD,AB=3