题目内容

不等式组
x-y-2≤0
x+2y-4≥0
2y-3≤0
所确定的平面区域记为D，当M（x，y）∈D时，A（-2，0），B（2，0），则
AM
•
BM
的最小值为（　　）
A、
13
2
-4
B、
4
5
5
-4
C、-
3
4
D、-
4
5
考点：简单线性规划
专题：不等式的解法及应用
分析：易知
AM
•
BM
表示区域D内的点M到原点距离的平方减掉4，由图象可得M到原点的最小距离为原点到直线x+2y-4=0的距离d，由点到直线的距离公式可求．
解答： 解：由题意作出区域D（阴影），
可得
AM
=（x+2，y），
BM
=（x-2，y），
∴
AM
•
BM
=（x+2）（x-2）+y2=x2+y2-4，
表示区域D内的点M到原点距离的平方减掉4，
由图象可得M到原点的最小距离为原点到直线x+2y-4=0的距离d，
由点到直线的距离公式可得d=
|0-2×0-4|
12+22
=
4
5
5
，
∴所求最小值为（
4
5
5
）2-4=-
4
5

故选：D
点评：本题考查简单线性规划，涉及点到直线的距离公式和向量的数量积运算，准确作图是解决问题的关键，属中档题．
练习册系列答案
相关题目
函数f（x）=3-|log2x|-4|x-1|的值域是
 
．
已知复数z=
3
2
i-
1
2
，则z的共轭复数为（　　）
A、
1
2
-
3
2
i
B、
1
2
+
3
2
i
C、-
1
2
-
3
2
i
D、-
1
2
+
3
2
i
从甲城市到乙城市m分钟的电话费由函数f（m）=1.06×（
3
4
[m]+
7
4
）给出，其中m＞0，[m]表示不大于m的最大整数（如[3]=3，[3.9]=3，[3.1]=3），则从甲城市到乙城市7.8分钟的电话费为
 
．
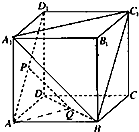如图，在棱长为a的正方体ABCD-A1B1C1D1中，P、Q分别是AD1、BD的中点．
（1）求证：PQ∥平面DCC1D1．
（2）求证：平面APQ∥平面A1C1B．
在三棱锥P-ABC中，平面PBC⊥平面ABC，AB=AC，E，F分别为BC，BP的中点，求证：（1）直线EF∥平面PAC；
（2）平面AEF⊥平面PBC．
有以下几种叙述：
①函数f（x）=|x+a|-|x-a|（a∈R）为奇函数；
②若函数y=f（x-1）是偶函数，则函数y=f（x）的图象关于直线x=-1对称；
③设（a，b），（c，d）都是函数f（x）的单调增区间（b＜c），且x1∈（a，b），x2∈（c，d），x1＜x2，则f（x1）＜f（x2）；
④已知函数f（x）=
-x2+2ax，
 (x≤1)
ax+1，(x＞1)
，若存在x1，x2∈R，且x1≠x2，使得f（x1）=f（x2）则实数a的取值范围是（-∞，1）∪（2，+∞）；
以上说法正确的是
 
．（写出你认为正确的所有命题的序号）
已知sin（α+
π
2
）=
1
3
，α∈(-
π
2
，0)，求tan（π-α）．
在数列{an}中，a1=1，a2=2，且an+2=an+1-an，设数列{an}的前n项和为Sn，则S2014=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网