题目内容
12．极坐标方程ρ2cos2θ+1=0表示的曲线是（ ）| A． | 圆 | B． | 椭圆 | C． | 双曲线 | D． | 抛物线 |
分析 利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，将其化为普通方程可得结论．
解答 解：由ρ2cos2θ+1=0，
可得：ρ2（2cos2θ-1）=-1，
得：2ρ2cos2θ=ρ2-1
2x2=x2+y2-1，即y2-x2=1，
∴极坐标方程ρ2cos2θ+1=0表示的曲线是等轴双曲线．
故选C
点评 本题考查点的极坐标和直角坐标的互化，比较基础．
练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
17．
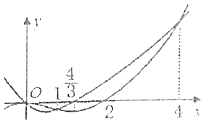已知函数f（x）与f'（x）的图象如图所示，则函数$g（x）=\frac{f（x）}{e^x}$的单调递增区间为（ ）
已知函数f（x）与f'（x）的图象如图所示，则函数$g（x）=\frac{f（x）}{e^x}$的单调递增区间为（ ）| A． | （0，4） | B． | $（{-∞，1}），（{\frac{4}{3}，4}）$ | C． | （0，1），（4，+∞） | D． | （-∞，0），（1，4） |
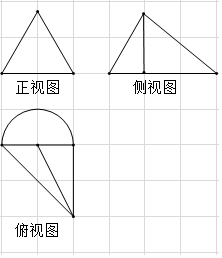
1．
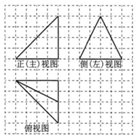在正方形网格中，某四面体的三视图如图所示．如果小正方形网格的边长为1，那么该四面体最长棱的棱长为（ ）
在正方形网格中，某四面体的三视图如图所示．如果小正方形网格的边长为1，那么该四面体最长棱的棱长为（ ）| A． | 4$\sqrt{3}$ | B． | 6 | C． | 4$\sqrt{2}$ | D． | 2$\sqrt{5}$ |