题目内容
1.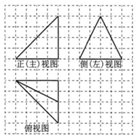 在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )
在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )| A. | 4$\sqrt{3}$ | B. | 6 | C. | 4$\sqrt{2}$ | D. | 2$\sqrt{5}$ |
分析 由已知中的三视图,可知该几何体是一个以边长为4的等腰直角三角形为底面,高为4的四面体,计算各条棱的长度可得答案.
解答  解:解:由三视图知:几何体是三棱锥,边长为4的等腰直角三角形为底面,高为4,(如图),
解:解:由三视图知:几何体是三棱锥,边长为4的等腰直角三角形为底面,高为4,(如图),
∵AC=4,BC=4,AC⊥BC,SO⊥BC,SO=4,OB=OC=2,
∴AB=4$\sqrt{2}$,AO=SB=SC=2$\sqrt{5}$,
AOS是三角形直角,∴AS=6.
∴棱的最长是AS=6,
故选:B.
点评 本题考查的知识点是三视图投影关系,根据已知的三视图,判断几何体的形状和尺寸关系是解答的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
12.极坐标方程ρ2cos2θ+1=0表示的曲线是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
16.已知全集 U={1,2,3,4,5,6},集合A={1,3,5},B={1,4},那么 A∩∁UB=( )
| A. | {3,5} | B. | {2,4,6} | C. | {1,2,4,6} | D. | {1,2,3,5,6} |
13.若集合A={1,2,3,4},B={x|x2-x-6≤0},则A∩B=( )
| A. | {1} | B. | {1,2} | C. | {2,3} | D. | {1,2,3} |
10.已知集合P={x|x2>2},Q={0,1,2,3},则(∁RP)∩Q=( )
| A. | {0,1} | B. | {0} | C. | {2,3} | D. | {1,2,3} |
11.设集合A={y|y=x2+2x-1,x∈R},B={x|x2-1≤0},则A∩B=( )
| A. | [-2,+∞) | B. | [-1,+∞) | C. | [-1,1] | D. | [-2,1] |