题目内容
3.如图,网络纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,其中正视图为等边三角形,则该几何体的体积为$\frac{(4+π)\sqrt{3}}{6}$.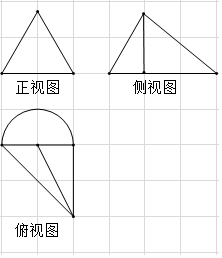
分析 由几何体的三视图知该几何体是一个底面半径为1、高为$\sqrt{3}$的半圆锥和底为两腰为2的等腰直角形高为$\sqrt{3}$的三棱锥的组合体,由此能求出该几何体的体积.
解答 解: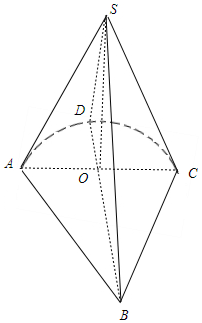 如图,由几何体的三视图知该几何体
如图,由几何体的三视图知该几何体
是一个底面半径为1、高为$\sqrt{3}$的半圆锥和底为两腰为2的等腰直角形
高为$\sqrt{3}$的三棱锥的组合体,
∴该几何体的体积:
V=V半圆锥S-ADC+V三棱锥S-ABC
=$\frac{1}{3}×\frac{1}{2}(π×{1}^{2})$×$\sqrt{3}$+$\frac{1}{3}×(\frac{1}{2}×2×2)×\sqrt{3}$
=$\frac{(4+π)\sqrt{3}}{6}$.
故答案为:$\frac{(4+π)\sqrt{3}}{6}$.
点评 本题考查几何体的体积的求法,考查三视图、半圆锥、三棱锥的性质等基础知识,考查推理论证能力、空间想象能力、运算求解能力,考查数形结合思想,是中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
19.函数$f(x)=Asin(ωx+φ),(ω>0,-\frac{π}{2}<φ<\frac{π}{2})$的部分图象如图所示,则A,ω,φ的值分别是( )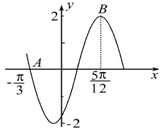

| A. | 1,$2,-\frac{π}{6}$ | B. | 2,$2,-\frac{π}{3}$ | C. | 1,$4,-\frac{π}{6}$ | D. | 2,$4,\frac{π}{3}$ |
18.在平面直角坐标系xOy中,已知成$\overrightarrow{OA}$=(-1,t),$\overrightarrow{OB}$=(2,2),若∠ABO=90°,则实数t的值为( )
| A. | 1 | B. | -3 | C. | $\frac{1}{3}$ | D. | 5 |
8.函数f(x)是定义在区间(0,+∞)上可导函数,其导函数为f'(x),且满足xf'(x)+2f(x)>0,则不等式$\frac{{({x+2017})f({x+2017})}}{5}$$<\frac{5f(5)}{x+2017}$的解集为( )
| A. | {x|x>-2012} | B. | {x|x<-2012} | C. | {x|-2012<x<0} | D. | {x|-2017<x<-2012} |
12.极坐标方程ρ2cos2θ+1=0表示的曲线是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
13.若集合A={1,2,3,4},B={x|x2-x-6≤0},则A∩B=( )
| A. | {1} | B. | {1,2} | C. | {2,3} | D. | {1,2,3} |