题目内容
17.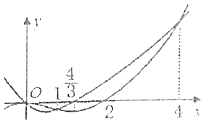 已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )
已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )| A. | (0,4) | B. | $({-∞,1}),({\frac{4}{3},4})$ | C. | (0,1),(4,+∞) | D. | (-∞,0),(1,4) |
分析 求出函数g(x)的导数,结合图象求出函数的递增区间即可.
解答 解:g′(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$,
由图象得:x<0,1<x<4时,f′(x)-f(x)>0,
故g(x)在(-∞,0),(1,4)递增,
故选:D.
点评 本题考查了函数的单调性问题,考查数形结合思想,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
7.某人提出一个问题,甲先答,答对的概率为0.4,如果甲答错,由乙答,答对的概率为0.5,则问题由乙答对的概率为 ( )
| A. | 0.2 | B. | 0.3 | C. | 0.4 | D. | 0.8 |
8.函数f(x)是定义在区间(0,+∞)上可导函数,其导函数为f'(x),且满足xf'(x)+2f(x)>0,则不等式$\frac{{({x+2017})f({x+2017})}}{5}$$<\frac{5f(5)}{x+2017}$的解集为( )
| A. | {x|x>-2012} | B. | {x|x<-2012} | C. | {x|-2012<x<0} | D. | {x|-2017<x<-2012} |
12.极坐标方程ρ2cos2θ+1=0表示的曲线是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
7.若复数z1,z2在复平面内的对应点关于虚轴对称,且z1=1+i,则z1•z2=( )
| A. | -2 | B. | 2 | C. | -2i | D. | 2i |