题目内容
18.下列命题中正确的有②④(填序号)①若-$\frac{π}{2}$<α<β<$\frac{π}{2}$,则α-β的取值范围为(-π,π);
②若α在第一象限,则$\frac{α}{2}$在第一、三象限;
③若sinθ=$\frac{m-3}{m+5}$,cosθ=$\frac{4-2m}{m+5}$,则m=8;
④若sin$\frac{θ}{2}$=$\frac{3}{5}$,cos$\frac{θ}{2}$=-$\frac{4}{5}$,则θ在第四象限.
分析 根据角的定义和三角函数符号判断.
解答 解:①∵α<β,∴α-β<0,故①错误;
②若α是第一象限角,则2kπ<α<$\frac{π}{2}+2kπ$,
∴kπ$<\frac{α}{2}<\frac{π}{4}+kπ$,∴$\frac{α}{2}$在第一、三象限.故②正确.
③∵sin2θ+cos2θ=1,∴($\frac{m-3}{m+5}$)2+($\frac{4-2m}{m+5}$)2=1,
解得m=0或m=8.故③错误.
④∵sin$\frac{θ}{2}$=$\frac{3}{5}$,cos$\frac{θ}{2}$=-$\frac{4}{5}$,∴$\frac{θ}{2}$=143°+360°•k
∴θ=286°+360°•2k.
∴θ在第四象限.故④正确.
故答案为:②④.
点评 本题考查了角的定义,象限角的三角函数的符号,属于基础题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
8.函数f(x)=-xcosx的图象为( )
| A. |  | B. |  | C. |  | D. |  |
9.设等差数列{an}的前n项和为Sn,若S6>S7>S5,则满足Sn<0的正整数n的最小值为( )
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
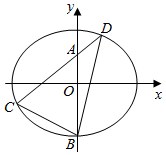 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.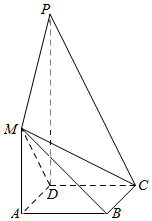 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.