题目内容
3.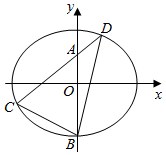 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.(Ⅰ)求椭圆E的标准方程;
(Ⅱ)若斜率为k的直线l过点A(0,1),且与椭圆E交于C,D两点,B为椭圆E的下顶点,求证:对于任意的k,直线BC,BD的斜率之积为定值.
分析 (Ⅰ)运用离心率公式和点满足椭圆方程,解得a,b,进而得到椭圆方程;
(Ⅱ)设直线l:y=kx+1,代入椭圆方程,运用韦达定理和直线的斜率公式,以及点在直线上满足直线方程,化简整理,即可得到定值.
解答 解:(Ⅰ)∵$e=\frac{{\sqrt{3}}}{3}$,∴$c=\frac{{\sqrt{3}}}{3}a$,∴${a^2}={b^2}+(\frac{{\sqrt{3}}}{3}a{)^2}$①,
又椭圆过点$(\sqrt{3},\sqrt{2})$,∴$\frac{3}{a^2}+\frac{2}{b^2}=1$②
由①②解得a2=6,b2=4,
所以椭圆E的标准方程为$\frac{x^2}{6}+\frac{y^2}{4}=1$;
(Ⅱ)证明:设直线l:y=kx+1,
联立$\left\{\begin{array}{l}\frac{x^2}{6}+\frac{y^2}{4}=1\\ y=kx+1\end{array}\right.$得:(3k2+2)x2+6kx-9=0,
设C(x1,y1),D(x2,y2),
则有${x_1}+{x_2}=-\frac{6k}{{3{k^2}+2}}$,${x_1}{x_2}=-\frac{9}{{3{k^2}+2}}$.
易知B(0,-2),
故${k_{BC}}•{k_{BD}}=\frac{{{y_1}+2}}{x_1}•\frac{{{y_2}+2}}{x_2}=\frac{{k{x_1}+3}}{x_1}•\frac{{k{x_2}+3}}{x_2}=\frac{{{k^2}{x_1}{x_2}+3k({x_1}+{x_2})+9}}{{{x_1}{x_2}}}$
=${k^2}+\frac{{3k({x_1}+{x_2})}}{{{x_1}{x_2}}}+\frac{9}{{{x_1}{x_2}}}={k^2}+3k•\frac{2k}{3}-(3{k^2}+2)=-2$为定值.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和点满足椭圆方程,考查直线方程和椭圆方程联立,运用韦达定理和直线的斜率公式,化简整理,考查运算能力,属于中档题.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案| A. | y=sin2x-cos2x | B. | y=cos2x-sin2x | C. | y=cos2x+sin2x | D. | y=cosxsinx |
| A. | “?a∈R,函数y=π”是减函数 | B. | “?a∈R,函数y=π”不是增函数 | ||
| C. | “?a∈R,函数y=π”不是增函数 | D. | “?a∈R,函数y=π”是减函数 |
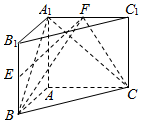 如图,直三棱柱ABC-A1B1C1中,AB⊥AC,E,F分别是BB1,A1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,E,F分别是BB1,A1C1的中点.