题目内容
15.若区间[x1,x2]的 长 度 定 义 为|x2-x1|,函数f(x)=$\frac{({m}^{2}+m)x-1}{{m}^{2}x}$(m∈R,m≠0)的定义域和值域都是[a,b],则区间[a,b]的最大长度为( )| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 3 |
分析 化简f(x),首先考虑f(x)的单调性,由题意:$\left\{\begin{array}{l}{f(a)=a}\\{f(b)=b}\end{array}\right.$,故a,b是方程f(x)的同号的相异实数根.利用韦达定理和判别式,求出a,b的关系,再求最大值.
解答 解:函数f(x)=$\frac{({m}^{2}+m)x-1}{{m}^{2}x}$(m∈R,m≠0)的定义域是{x|x≠0},则[m,n]是其定义域的子集,
∴[m,n]⊆(-∞,0)或(0,+∞).
f(x)=$\frac{({m}^{2}+m)x-1}{{m}^{2}x}$=$\frac{m+1}{m}$-$\frac{1}{{m}^{2}x}$在区间[a,b]上时增函数,
则有:$\left\{\begin{array}{l}{f(a)=a}\\{f(b)=b}\end{array}\right.$,
故a,b是方程f(x)=$\frac{m+1}{m}$-$\frac{1}{{m}^{2}x}$=x的同号相异的实数根,
即a,b是方程(mx)2-(m2+m)x+1=0同号相异的实数根.
那么ab=$\frac{1}{{m}^{2}}$,a+b=$\frac{m+1}{m}$,只需要△>0,
即(m2+m)2-4m2>0,解得:m>1或m<-3.
那么:n-m=$\sqrt{{(a+b)}^{2}-4ab}$=$\sqrt{-{3(\frac{1}{m}-\frac{1}{3})}^{2}+\frac{4}{3}}$,
故b-a的最大值为$\frac{2\sqrt{3}}{3}$,
故选:A.
点评 本题考查了函数性质的方程的运用,有一点综合性,利用函数关系,构造新的函数解题.属于中档题,分类讨论思想的运用,增加了本题的难度,解题时注意.

 阅读快车系列答案
阅读快车系列答案| A. | 66 | B. | 99 | C. | 144 | D. | 297 |
| A. | c<b<a | B. | a<b<c | C. | c<a<b | D. | b<a<c |
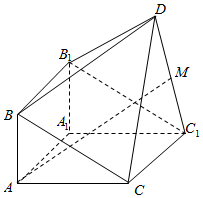 如图,由直三棱柱ABC-A1B1C1和四棱锥D-BB1C1C构成的几何体中,∠BAC=90°,AB=1,BC=BB1=2,C1D=CD=$\sqrt{5}$,平面CC1D⊥平面ACC1A1.
如图,由直三棱柱ABC-A1B1C1和四棱锥D-BB1C1C构成的几何体中,∠BAC=90°,AB=1,BC=BB1=2,C1D=CD=$\sqrt{5}$,平面CC1D⊥平面ACC1A1. ,则
,则 的值等于
的值等于 B.
B. C.0 D.
C.0 D.