题目内容
根据以下向量组①②③的坐标计算并猜想向量
=(cos10°,sin10°)与
=(cos50°,sin50°)夹角为 .
①
=(cos30°,shi30°),
=(cos60°,sin60°)
②
=(cos75°,shi75°),
=(cos15°,sin15°)
③
=(cos45°,shi45°),
=(cos90°,sin90°)
| a |
| b |
①
| a |
| b |
②
| a |
| b |
③
| a |
| b |
考点:归纳推理
专题:推理和证明
分析:设向量的夹角为θ,根据cosθ=
,分别求出①②③的夹角,可以发现其夹角等于两个度数之差(大的度数减去小的度数).
| ||||
|
|
解答:
解:设向量的夹角为θ,根据cosθ=
,而|
|=1,|
|=1
①
=(cos30°,sin30°),
=(cos60°,sin60°),
∴
•
=cos30°cos60°+sin30°sin60°=cos30°sin30°+sin30°cos30°=sin(30°+30°)=sin60°=
,∴cosθ=
,∴θ=30°=60°-30°,
②
=(cos75°,sin75°),
=(cos15°,sin15°)
∴
•
=cos75°cos15°+sin75°sin15°=cos75°sin75°+sin75°cos75°=sin(75°+75°)=sin150°=
,∴cosθ=
,∴θ=60°=75°-15°,
同理③
=(cos45°,shi45°),
=(cos90°,sin90°),θ=45°=90°-45°=45°.
由以上可得,
=(cos10°,sin10°)与
=(cos50°,sin50°)夹角为50°-10°=40°.
故答案为:40°.
| ||||
|
|
| a |
| b |
①
| a |
| b |
∴
| a |
| b |
| ||
| 2 |
| ||
| 2 |
②
| a |
| b |
∴
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
同理③
| a |
| b |
由以上可得,
| a |
| b |
故答案为:40°.
点评:本题主要考查向量的夹角公式,三角函数的和差公式,以及归纳推理的问题,关键是找到规律,属于基础题.

练习册系列答案
相关题目
已知某产品的广告费x与销售额y回归直线方程为
=9.4x+9.1,据此模型预报广告费为6万元时的销售额( )
 |
| y |
| A、72.0 | B、66.2 |
| C、67.7 | D、65.5 |
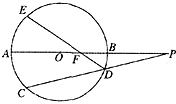 已知⊙O的半径R=2,P为直径AB延长线上一点,PB=3,割线PDC交⊙O于D,C两点,E为⊙O上一点,且
已知⊙O的半径R=2,P为直径AB延长线上一点,PB=3,割线PDC交⊙O于D,C两点,E为⊙O上一点,且