题目内容
函数y=sin(-2x+
)的单调递减区间是 .
| 5π |
| 6 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:根据y=sin(-2x+
)=-sin(2x-
),故本题即求函数y=sin(2x-
)的单调递增区间.令2kπ-
≤2x-
≤2x+
,k∈z,求得x的范围,可得函数y=sin(2x-
)的单调递增区间.
| 5π |
| 6 |
| 5π |
| 6 |
| 5π |
| 6 |
| π |
| 2 |
| 5π |
| 6 |
| π |
| 2 |
| 5π |
| 6 |
解答:
解:函数y=sin(-2x+
)=-sin(2x-
)的单调递减区间,
即函数y=sin(2x-
)的单调递增区间.
令2kπ-
≤2x-
≤2x+
,k∈z,求得 kπ+
≤x≤kπ+
,
故函数y=sin(-2x+
)的单调递减区间是[kπ+
,kπ+
],k∈z
故答案为:[kπ+
,kπ+
],k∈z.
| 5π |
| 6 |
| 5π |
| 6 |
即函数y=sin(2x-
| 5π |
| 6 |
令2kπ-
| π |
| 2 |
| 5π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
故函数y=sin(-2x+
| 5π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
故答案为:[kπ+
| π |
| 6 |
| 2π |
| 3 |
点评:本题主要考查正弦函数的单调性,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
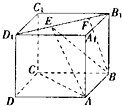 如图正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E、F,且EF=
如图正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E、F,且EF=| 1 |
| 2 |
| A、AC⊥BE |
| B、EF∥平面ABCD |
| C、三棱锥A-BEF的体积为定值 |
| D、△AEF的面积与△BEF的面积相等 |
已知实数x,y满足
,则Z=2x-y的最小值是( )
|
| A、3 | B、-3 | C、5 | D、-5 |
 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a11,4为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a11,4为