题目内容
下列命题:
①△ABC中,若A<B,则cos2A<cos2B;
②若A,B,C为△ABC的三个内角,则
+
的最小值为
③已知an=sin
+
(n∈N*),则数列{an}中的最小项为
;
④若函数f(x)=log2(x+1),且0<a<b<c,则
<
<
;
其中所有正确命题的序号是 .
①△ABC中,若A<B,则cos2A<cos2B;
②若A,B,C为△ABC的三个内角,则
| 4 |
| A |
| 1 |
| B+C |
| 9 |
| π |
③已知an=sin
| nπ |
| 6 |
| 16 | ||
2+sin
|
| 19 |
| 3 |
④若函数f(x)=log2(x+1),且0<a<b<c,则
| f(a) |
| a |
| f(b) |
| b |
| f(c) |
| c |
其中所有正确命题的序号是
考点:命题的真假判断与应用
专题:综合题,函数的性质及应用,点列、递归数列与数学归纳法,解三角形
分析:①△ABC中,由大角对大边和正弦定理得出sinA<sinB,再由三角恒等变换得出cos2A>cos2B,判定①是否正确;
②△ABC中,由A+B+C=π得出
=1,求出
+
的最小值即可判定②是否正确;
③设f(x)=x+
,x∈[-1,1],求出x=1时f(x)取得最小值
,判定数列{an}有最小项;得出③正确;
④画出函数f (x)=log2(x+1)的图象,结合图形以及
的几何意义,判定④是否正确.
②△ABC中,由A+B+C=π得出
| A+B+C |
| π |
| 4 |
| A |
| 1 |
| B+C |
③设f(x)=x+
| 16 |
| 2+x |
| 19 |
| 3 |
④画出函数f (x)=log2(x+1)的图象,结合图形以及
| f(x) |
| x |
解答:
解:对于①,△ABC中,A<B时,a<b,即sinA<sinB,∴sin2A<sin2B,∴1-2sin2A>1-2sin2B,即cos2A>cos2B,∴①错误;
对于②,△ABC中,A+B+C=π,∴
=1,∴
+
=(
+
)•
=
[4+1+
+
]≥
[5+2
]=
;
当且仅当A=2(B+C),即A=
时,“=”成立,即取最小值
;∴②正确;
对于③,设f(x)=x+
,x∈[-1,1],∴f′(x)=1-
;当x∈[-1,1]时,f′(x)<0,f(x)是减函数;∴x=1,f(x)取得最小值1+
=
;
即sin
=1,n=3+12k(k∈N*)时,数列{an}有最小项为
;∴③正确;
对于④,画出函数f (x)=log2(x+1)的图象,如图所示 :
:
令g(x)=
=
,其几何意义是f(x)图象上的点(x,f(x))与原点连线的斜率,
由图知函数g(x)为(-1,+∞)上的减函数,∵0<a<b<c,∴
>
>
;∴④错误;
综上,以上正确的命题是②③.
故答案为:②③.
对于②,△ABC中,A+B+C=π,∴
| A+B+C |
| π |
| 4 |
| A |
| 1 |
| B+C |
| 4 |
| A |
| 1 |
| B+C |
| A+B+C |
| π |
| 1 |
| π |
| 4(B+C) |
| A |
| A |
| B+C |
| 1 |
| π |
|
| 9 |
| π |
当且仅当A=2(B+C),即A=
| 2π |
| 3 |
| 9 |
| π |
对于③,设f(x)=x+
| 16 |
| 2+x |
| 16 |
| (x+2)2 |
| 16 |
| 2+1 |
| 19 |
| 3 |
即sin
| nπ |
| 6 |
| 19 |
| 3 |
对于④,画出函数f (x)=log2(x+1)的图象,如图所示
 :
:令g(x)=
| f(x) |
| x |
| f(x)-0 |
| x-0 |
由图知函数g(x)为(-1,+∞)上的减函数,∵0<a<b<c,∴
| f(a) |
| a |
| f(b) |
| b |
| f(c) |
| c |
综上,以上正确的命题是②③.
故答案为:②③.
点评:本题通过命题真假的判定,考查了解三角形的知识,三角函数的图象与性质,三角恒等变换,数列的应用,基本不等式的应用,函数的图象与性质等知识,是综合性题目.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
从学号为0~50的燕中高二某班50名学生中随机选取5名同学参加数学测试,采用系统抽样的方法,则所选5名学生的学号可能是( )
| A、1,2,3,4,5 |
| B、5,16,27,38,49 |
| C、2,4,6,8,10 |
| D、4,13,22,31,40 |
函数y=
的图象如图所示,则( )
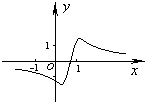
| 2(x+a) |
| (x+a)2+b |

| A、a∈(0,1),b∈(0,1) |
| B、a∈(0,1),b∈(1,+∞) |
| C、a∈(-1,0),b∈(1,+∞) |
| D、a∈(-1,0),b∈(0,1) |
 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a11,4为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.则a11,4为