题目内容
已知某产品的广告费x与销售额y回归直线方程为
=9.4x+9.1，据此模型预报广告费为6万元时的销售额（ ）
 |
| y |
| A、72.0 | B、66.2 |
| C、67.7 | D、65.5 |
考点：线性回归方程
专题：计算题,概率与统计
分析：利用线性回归方程，把自变量为6代入，预报出结果．
解答：
解：∵线性回归方程是y=9.4x+9.1，
∴广告费用为6万元时销售额为9.4×6+9.1=65.5，
故选D．
∴广告费用为6万元时销售额为9.4×6+9.1=65.5，
故选D．
点评：本题考查线性回归方程．考查预报变量的值，本题是一个基础题．
练习册系列答案
相关题目
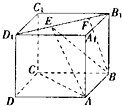如图正方体ABCD-A1B1C1D1的棱长为2，线段B1D1上有两个动点E、F，且EF=| 1 |
| 2 |
| A、AC⊥BE |
| B、EF∥平面ABCD |
| C、三棱锥A-BEF的体积为定值 |
| D、△AEF的面积与△BEF的面积相等 |
在△ABC中，∠A、∠B、∠C所对的边分别是2、3、4，则三角形中最大角的余弦值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、-
|
下列各式中最小值为2的是（ ）
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、sinx+
|
函数y=
的图象如图所示，则（ ）
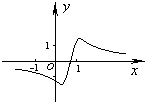
| 2(x+a) |
| (x+a)2+b |
| A、a∈（0，1），b∈（0，1） |
| B、a∈（0，1），b∈（1，+∞） |
| C、a∈（-1，0），b∈（1，+∞） |
| D、a∈（-1，0），b∈（0，1） |
已知实数x，y满足
，则Z=2x-y的最小值是（ ）
|
| A、3 | B、-3 | C、5 | D、-5 |
下列函数中，最小正周期为π的是（ ）
| A、y=|sinx| | ||
| B、y=sinx | ||
C、y=tan
| ||
| D、y=cos4x |
有A、B两个口袋，A袋装有4个白球，2个黑球；B袋装有3个白球，4个黑球，从A袋、B袋各取2个球交换之后，则A袋中装有4个白球的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|