题目内容
 已知椭圆:
已知椭圆:| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆的方程;
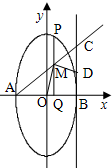
(Ⅱ)试判断O、B、D、M四点是否共圆,并说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
,由此能求出椭圆的方程.
(Ⅱ)O、B、D、M四点共圆,且圆心为OD的中点.由已知条件得到A(-1,0),B(1,0),直线l:x=1.
设点P(x0,y0),推导出M(x0,
),C(1,
),D(1,
),由此利用直角三角形性质能证明O、B、D、M在以N为圆心的圆上.
|
(Ⅱ)O、B、D、M四点共圆,且圆心为OD的中点.由已知条件得到A(-1,0),B(1,0),直线l:x=1.
设点P(x0,y0),推导出M(x0,
| y0 |
| 2 |
| y0 |
| x0+1 |
| y0 |
| 2(x0+1) |
解答:
解:(Ⅰ)∵椭圆:
+
=1(a>b>0)的离心率e=
,
椭圆左右顶点分别为A、B,且A到椭圆两焦点的距离之和为4,
∴
,解得a=2,b=1,
∴椭圆的方程为
+x2=1.…(4分)
(Ⅱ)O、B、D、M四点共圆,且圆心为OD的中点.…(5分)
证明如下:
∵椭圆
+x2=1左右顶点分别为A、B,
∴A(-1,0),B(1,0),直线l:x=1.
设点P(x0,y0),则点M(x0,
).…(6分)
直线AM:y=
(x+1),令x=1,得C(1,
),
∴D(1,
)…(8分)
∴
=(x0,
),
=(x0-1,
-
)=(x0-1,
)…(10分)
∴
•
=(x0,
)•(x0-1,
)=x0(x0-1)+
=
,(12分)
∵点P(x0,y0),∴4
+
=4,
∴
•
=0,∴∠OMD=90°.…(13分)
∴△OMD和△OBD都是直角三角形,
取OD中点N,则由直角三角形性质知|NO|=|NB|=|ND|=|NM|,
∴O、B、D、M在以N为圆心的圆上.…(14分)
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
椭圆左右顶点分别为A、B,且A到椭圆两焦点的距离之和为4,
∴
|
∴椭圆的方程为
| y2 |
| 4 |
(Ⅱ)O、B、D、M四点共圆,且圆心为OD的中点.…(5分)
证明如下:
∵椭圆
| y2 |
| 4 |
∴A(-1,0),B(1,0),直线l:x=1.
设点P(x0,y0),则点M(x0,
| y0 |
| 2 |
直线AM:y=
| y0 |
| 2(x0+1) |
| y0 |
| x0+1 |
∴D(1,
| y0 |
| 2(x0+1) |
∴
| OM |
| y0 |
| 2 |
| DM |
| y0 |
| 2 |
| y0 |
| 2(x0+1) |
| x0y0 |
| 2(x0+1) |
∴
| OM |
| DM |
| y0 |
| 2 |
| x0y0 |
| 2(x0+1) |
x0
| ||
| 4(x0+1) |
x0(4
| ||||
| 4(x0+1) |
∵点P(x0,y0),∴4
| x | 2 0 |
| y | 2 0 |
∴
| OM |
| DM |
∴△OMD和△OBD都是直角三角形,
取OD中点N,则由直角三角形性质知|NO|=|NB|=|ND|=|NM|,
∴O、B、D、M在以N为圆心的圆上.…(14分)
点评:本题考查椭圆方程的求法,考查四点共圆的判断与证明,解题时要熟练掌握椭圆的简单性质,注意等价转化思想的合理运用.

练习册系列答案
相关题目
函数f(x)=2x2-mx+5,当x∈[-1,+∞)时是增函数,当x∈(-∞,-1]时是减函数,则f(-2)等于( )
| A、5 | B、7 |
| C、9 | D、由m的值而定的常数 |
已知a,b是异面直线,则下面四个命题:
①过直线a至少有一个平面平行于b;
②在空间中至少有一个平面分别与a,b都平行;
③在空间中至多有一条直线与a,b都相交.
其中正确命题的个数是( )
①过直线a至少有一个平面平行于b;
②在空间中至少有一个平面分别与a,b都平行;
③在空间中至多有一条直线与a,b都相交.
其中正确命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
阅读如图所示程序框图,运行相应的程序,输出s的值等于( )
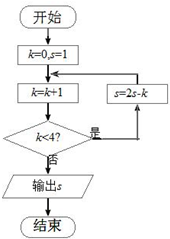

| A、-3 | B、-10 | C、0 | D、-2 |
 如图,抛物线C的顶点为O(0,0),焦点在y轴上,抛物线上的点(x0,1)到焦点的距离为2.
如图,抛物线C的顶点为O(0,0),焦点在y轴上,抛物线上的点(x0,1)到焦点的距离为2.