题目内容
将函数f(x)=
sin2x-cos2x的图象向左平移m个单位(m>0),若所得的图象关于直线x=
对称,则m的最小值为( )
| 3 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:首先通过三角函数的恒等变换,变换成正弦型函数,进一步利用平移变换,最后根据正弦型函数的对称轴求得结果.
解答:
解:函数f(x)=
sin2x-cos2x=2sin(2x-
)的图象向左平移m个单位,得到
g(x)=2sin(2x+2m-
)
所得的图象关于直线x=
对称,
则:2×
+2m-
=kπ+
(k∈Z)
即:m=
+
当k=0时,m=
故选:A
| 3 |
| π |
| 6 |
g(x)=2sin(2x+2m-
| π |
| 6 |
所得的图象关于直线x=
| π |
| 6 |
则:2×
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
即:m=
| kπ |
| 2 |
| π |
| 6 |
当k=0时,m=
| π |
| 6 |
故选:A
点评:本题考查的知识要点:三角函数的恒等变换,函数图象的平移变换问题,及对称轴问题,属于基础题型.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
下列图象中最左边是高青到张店71路公共汽车收支差额y与乘客量x的图象,则图①图②图③的实线所表达的实际意义是( )
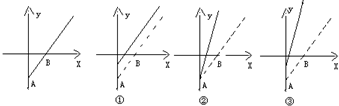

| A、①是票价不变降低成本,②是成本不变提高票价,③是降低成本提高票价 |
| B、①是成本不变提高票价,②是票价不变降低成本,③是降低成本提高票价 |
| C、①是降低成本提高票价,②是票价不变降低成本,③是票价不变降低成本 |
| D、①是成本不变提高票价,②是降低成本提高票价,③是降低成本提高票价 |
圆x2+y2+2x+4y-3=1到直线x+y+1=0距离为
的点共有( )
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
函数y=2x-5在R上的单调性是( )
| A、增函数 | B、减函数 |
| C、不增不减 | D、无法确定 |
