题目内容
若动点P到定点F(1,0)的距离比到直线x=-2距离小1,求点P的轨迹方程.
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:设点P的坐标为(x,y),利用已知条件列出方程
+1=|x-(-2)|,化简求解即可.
| (x-1)2+y2 |
解答:
解:设点P的坐标为(x,y),(2分)
则点P满足集合{P||PF|+1=d} (3分)
+1=|x-(-2)|(4分)
由图可知x>-2,故方程可化为
+1=x+2(6分)
两边平方得(x-1)2+y2=(x+1)2
整理得y2=4x((x≥0)(8分)
则点P满足集合{P||PF|+1=d} (3分)
| (x-1)2+y2 |
由图可知x>-2,故方程可化为
| (x-1)2+y2 |
两边平方得(x-1)2+y2=(x+1)2
整理得y2=4x((x≥0)(8分)
点评:本题考查轨迹方程的求法,基本知识的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在约束条件
下,若目标函数z=3x+2y的最大值的变化范围是[6,8],则实数m的取值范围是( )
|
| A、[3,8) |
| B、[3,+∞) |
| C、[2,8] |
| D、[2,+∞) |
将函数f(x)=
sin2x-cos2x的图象向左平移m个单位(m>0),若所得的图象关于直线x=
对称,则m的最小值为( )
| 3 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
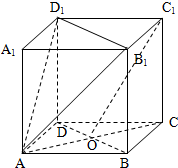 已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点,
已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点,