题目内容
已知f（x）是奇函数，g（x）是偶函数，则（ ）
| A、f（x）g（x）是偶函数 |
| B、f（x）g（x）是奇函数 |
| C、f（x）+g（x）是偶函数 |
| D、f（x）+g（x）是奇函数 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据函数的奇偶性和题意可得：f（-x）=-f（x），g（-x）=g（x），再由函数的奇偶性的定义判断函数
f（x）g（x）和f（x）+g（x）的奇偶性即可．
f（x）g（x）和f（x）+g（x）的奇偶性即可．
解答：
解：因为f（x）是奇函数，g（x）是偶函数，
所以f（-x）=-f（x），g（-x）=g（x），
则f（-x）g（-x）=-f（x）g（x），所以f（x）g（x）是奇函数；
f（-x）+g（-x）=-f（x）+g（x），所以f（x）+g（x）是非奇非偶函数，
所以A、C、D错误，B正确，
故选：B．
所以f（-x）=-f（x），g（-x）=g（x），
则f（-x）g（-x）=-f（x）g（x），所以f（x）g（x）是奇函数；
f（-x）+g（-x）=-f（x）+g（x），所以f（x）+g（x）是非奇非偶函数，
所以A、C、D错误，B正确，
故选：B．
点评：本题考查函数奇偶性的定义以及性质的应用，属于基础题．
练习册系列答案
相关题目
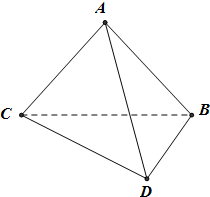如图，将一副三角板拼接，使他们有公共边BC，且使这两个三角形所在的平面互相垂直，∠BAC=∠CBD=90°，AB=AC，∠BCD=30°，BC=6．