题目内容
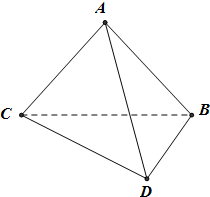 如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.
如图,将一副三角板拼接,使他们有公共边BC,且使这两个三角形所在的平面互相垂直,∠BAC=∠CBD=90°,AB=AC,∠BCD=30°,BC=6.(1)证明:平面ADC⊥平面ADB;
(2)求二面角A-CD-B平面角的正切值.
考点:二面角的平面角及求法,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知得BD⊥面ABC,BD⊥AC,从而AC⊥面ADB,由此能证明面ADC⊥面ADB.
(2)取BC的中点E,连接AE,则AE⊥BC,从而AE⊥面BCD,过E作EF⊥DC于F,连接AF,则∠AFE是二面角A-CD-B的平面角,由此能求出二面角A-CD-B平面角的正切值.
(2)取BC的中点E,连接AE,则AE⊥BC,从而AE⊥面BCD,过E作EF⊥DC于F,连接AF,则∠AFE是二面角A-CD-B的平面角,由此能求出二面角A-CD-B平面角的正切值.
解答:
(本小题满分14分)
(1)证明:因为面ABC⊥面BCD,BD⊥BC,
面ABC∩面BCD=BC,BD?面BCD,
所以BD⊥面ABC.(3分)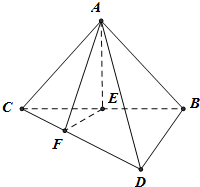
又AC?面ABC,所以BD⊥AC.(4分)
又AB⊥AC,且BD∩AB=B,
所以AC⊥面ADB.(5分)
又AC?面ADC,所以面ADC⊥面ADB.(6分)
(2)解:取BC的中点E,连接AE,则AE⊥BC,(7分)
又面ABC⊥面BCD,面ABC∩面BCD=BC,
所以AE⊥面BCD,(8分)
所以AE⊥CD,过E作EF⊥DC于F,连接AF,
则DC⊥面AEF,则DC⊥AF,所以∠AFE是二面角A-CD-B的平面角.(11分)
在Rt△CEF中,∠ECF=300,EF=
CE=
,又AE=3,(13分)
所以tan∠AFE=
=2,
即二面角A-CD-B平面角的正切值为2.(14分)
(1)证明:因为面ABC⊥面BCD,BD⊥BC,
面ABC∩面BCD=BC,BD?面BCD,
所以BD⊥面ABC.(3分)

又AC?面ABC,所以BD⊥AC.(4分)
又AB⊥AC,且BD∩AB=B,
所以AC⊥面ADB.(5分)
又AC?面ADC,所以面ADC⊥面ADB.(6分)
(2)解:取BC的中点E,连接AE,则AE⊥BC,(7分)
又面ABC⊥面BCD,面ABC∩面BCD=BC,
所以AE⊥面BCD,(8分)
所以AE⊥CD,过E作EF⊥DC于F,连接AF,
则DC⊥面AEF,则DC⊥AF,所以∠AFE是二面角A-CD-B的平面角.(11分)
在Rt△CEF中,∠ECF=300,EF=
| 1 |
| 2 |
| 3 |
| 2 |
所以tan∠AFE=
| AE |
| EF |
即二面角A-CD-B平面角的正切值为2.(14分)
点评:本题考查平面与平面垂直的证明,考查二面角的正切值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“x=0”是“x2+y2=0”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知f(x)是奇函数,g(x)是偶函数,则( )
| A、f(x)g(x)是偶函数 |
| B、f(x)g(x)是奇函数 |
| C、f(x)+g(x)是偶函数 |
| D、f(x)+g(x)是奇函数 |
f(x)=
在( )
| x |
| 1-x |
| A、(-∞,1)∪(1,+∞)上是增函数 |
| B、(-∞,1)∪(1,+∞)上是减函数 |
| C、(-∞,1),(1,+∞)分别是增函数 |
| D、(-∞,1),(1,+∞)分别是减函数 |
执行如图所示的程序框图输出的结果是( )


| A、8 | B、6 | C、5 | D、3 |