题目内容
已知对数函数f(x)=logax(a>0且a≠1)的图象过点(
,3)
(1)求f(x)的解析式,并求f(1),f(16),f(
)的值;
(2)已知f(x-1)>f(8-2x),求x的取值范围.
| 1 |
| 8 |
(1)求f(x)的解析式,并求f(1),f(16),f(
| 2 |
(2)已知f(x-1)>f(8-2x),求x的取值范围.
考点:对数函数的图像与性质
专题:计算题,函数的性质及应用
分析:(1)由题意知得到f(
)=loga
=3,从而求a及函数值;
(2)易知f(x)=-log2x是定义在(0,+∞)上的单调递减函数,从而由单调性求解不等式的解.
| 1 |
| 8 |
| 1 |
| 8 |
(2)易知f(x)=-log2x是定义在(0,+∞)上的单调递减函数,从而由单调性求解不等式的解.
解答:
解:(1)由题意知,f(
)=loga
=3;
解得,a=
;
故f(x)=-log2x;
故f(1)=0,f(16)=-log216=-4,f(
)=-log2
=-
;
(2)∵f(x)=-log2x是定义在(0,+∞)上的单调递减函数,
又∵f(x-1)>f(8-2x),
∴0<x-1<8-2x;
解得,1<x<3.
| 1 |
| 8 |
| 1 |
| 8 |
解得,a=
| 1 |
| 2 |
故f(x)=-log2x;
故f(1)=0,f(16)=-log216=-4,f(
| 2 |
| 2 |
| 1 |
| 2 |
(2)∵f(x)=-log2x是定义在(0,+∞)上的单调递减函数,
又∵f(x-1)>f(8-2x),
∴0<x-1<8-2x;
解得,1<x<3.
点评:本题考查了对数函数的性质与应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若函数y=ax+b的部分图象如图所示,则( )
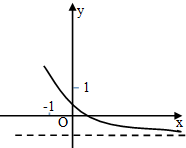

| A、0<a<1,-1<b<0 |
| B、0<a<1,0<b<1 |
| C、a>1,-1<b<0 |
| D、a>1,-1<b<0 |
二项式(1+x)n的展开式中,只有第七项的二项式系数最大,那么正整数n的值为( )
| A、10 | B、11 | C、12 | D、13 |
已知实数x,y满足不等式组
,则x+2y的最大值为( )
|
| A、3 | B、3 | C、4 | D、5 |
函数f(x)=lgx-
的零点所在的区间是( )
| 1 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,10) |
已知两条直线ax-y-2=0和(a+2)x-y+1=0互相垂直,则a的值等于( )
| A、2 | B、1 | C、0 | D、-1 |
已知集合A={x|y=lnx},集合B={-2,-1,0,1,2},则A∩B=( )
| A、(0,2) |
| B、{1,2} |
| C、(0,2) |
| D、{0,1,2} |