题目内容
已知函数f(x)=2cos(2x+
)+
sin2x
(1)求函数f(x)的最小正周期和最大值;
(2)设△ABC的三内角分别是A、B、C.若f(
)=
,且AC=1,BC=3,求边AB和sinA的值.
| π |
| 3 |
| 3 |
(1)求函数f(x)的最小正周期和最大值;
(2)设△ABC的三内角分别是A、B、C.若f(
| C |
| 2 |
| 1 |
| 2 |
考点:余弦定理的应用,三角函数中的恒等变换应用
专题:三角函数的图像与性质,解三角形
分析:(1)由两角和的余弦公式化简解析式可得f(x)=cos2x,从而可求最小正周期和最大值;
(2)由已知先求得cosC的值,即可求sinC的值,由余弦定理可得AB的值,从而由正弦定理得sinA的值.
(2)由已知先求得cosC的值,即可求sinC的值,由余弦定理可得AB的值,从而由正弦定理得sinA的值.
解答:
解:(1)∵f(x)=2cos(2x+
)+
sin2x=2(cos2xcos
-sin2xsin
)+
sin2x=cos2x
∴T=
=π
∴f(x)max=1
(2)∵f(x)=cos2x,
∴f(
)=cosC=
,可得:cosC=
.
∴sinC=
=
∴由余弦定理可得:AB2=BC2+AC2-2×AC×BC×cosC=9+1-2×1×3×
=7,即得AB=
∴由正弦定理:
=
可得:sinA=
=
=
.
| π |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
∴T=
| 2π |
| 2 |
∴f(x)max=1
(2)∵f(x)=cos2x,
∴f(
| C |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴sinC=
| 1-cos2C |
| ||
| 2 |
∴由余弦定理可得:AB2=BC2+AC2-2×AC×BC×cosC=9+1-2×1×3×
| 1 |
| 2 |
| 7 |
∴由正弦定理:
| BC |
| sinA |
| AB |
| sinC |
| BC•sinC |
| AB |
3×
| ||||
|
3
| ||
| 14 |
点评:本题主要考察了三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦定理、余弦定理的综合应用,综合性较强,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
在△ABC中,若S△ABC=
(a2+b2-c2),那么C等于( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=x2+bx+1在区间(0,1)和(1,2)上各有一个零点,则b的取值范围是( )
| A、(-∞,-2) | ||
B、(-
| ||
C、(-
| ||
D、(-∞,-
|
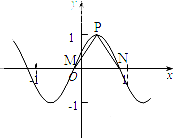 已知函数f(x)=
已知函数f(x)=
| ||
| 2 |
| 1 |
| 2 |
| PM |
| PN |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
为偶函数,则括号内应该填写的是( )
|
| A、x2+3x-2 |
| B、x2-3x-2 |
| C、-x2+3x-2 |
| D、-x2+3x+2 |
已知等比数列{an}的前n项和为Sn,且满足
=2,则公比q=( )
| S8 |
| S4 |
| A、±2 | B、±1 | C、-1 | D、1 |