题目内容
已知a1=2,a2=4,bn=an+1-an,bn+1=2bn+2.求证:
(1)数列{bn+2}是公比为2的等比数列;
(2)an=2n+1-2n;
(3)a1+a2+…+an=2n+2-n(n+1)-4.
(1)数列{bn+2}是公比为2的等比数列;
(2)an=2n+1-2n;
(3)a1+a2+…+an=2n+2-n(n+1)-4.
考点:数列递推式,等比关系的确定,数列的求和
专题:等差数列与等比数列
分析:(1)由bn+1=2bn+2,变形为bn+1+2=2(bn+2),即可证明;
(2)由(1)可得:bn+2=4×2n-1,an+1-an=2n+1-2,利用“累加求和”及其等比数列的前n项和公式即可得出.
(3)利用等比数列与等差数列的前n项和公式即可得出.
(2)由(1)可得:bn+2=4×2n-1,an+1-an=2n+1-2,利用“累加求和”及其等比数列的前n项和公式即可得出.
(3)利用等比数列与等差数列的前n项和公式即可得出.
解答:
证明:(1)∵bn+1=2bn+2,∴bn+1+2=2(bn+2),
b1=a2-a1=4-2=2.b1+2=4.
∴数列{bn+2}是公比为2的等比数列,首项为4;
(2)由(1)可得:bn+2=4×2n-1,
∴an+1-an=2n+1-2,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=(2n-2)+(2n-1-2)+…+(22-2)+2
=
-2(n-1)
=2n+1-2n.
∴an=2n+1-2n;
(3)a1+a2+…+an=
-2×
=2n+2-n(n+1)-4.
b1=a2-a1=4-2=2.b1+2=4.
∴数列{bn+2}是公比为2的等比数列,首项为4;
(2)由(1)可得:bn+2=4×2n-1,
∴an+1-an=2n+1-2,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=(2n-2)+(2n-1-2)+…+(22-2)+2
=
| 2(2n-1) |
| 2-1 |
=2n+1-2n.
∴an=2n+1-2n;
(3)a1+a2+…+an=
| 4(2n-1) |
| 2-1 |
| n(n+1) |
| 2 |
点评:本题考查了“累加求和”、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
若函数f(x)=x2+bx+1在区间(0,1)和(1,2)上各有一个零点,则b的取值范围是( )
| A、(-∞,-2) | ||
B、(-
| ||
C、(-
| ||
D、(-∞,-
|
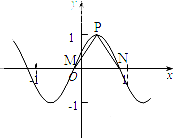 已知函数f(x)=
已知函数f(x)=
| ||
| 2 |
| 1 |
| 2 |
| PM |
| PN |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1的焦点到其渐近线的距离等于2,抛物线y2=2px的焦点为双曲线的右焦点,双曲线截抛物线的准线所得的线段长为4,则抛物线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、y2=4x | ||
B、y2=4
| ||
C、y2=8
| ||
| D、y2=8x |