题目内容
将三个半径为3的球两两相切地放在水平桌面上,若在这三个球的上方放置一个半径为1的小球,使得这四个球两两相切,则该小球的球心到桌面的距离为 .
考点:组合几何体的面积、体积问题
专题:空间位置关系与距离
分析:设四个球的球心分别为O1、O2、O3、O4,将它们两两连结恰好组成一个正三棱锥,且底面各棱长均为6,侧棱长均为4,作O1H⊥面O2O3O4,垂足为H,则O1H为棱锥的高,由此可求上面一个球的球心到桌面的距离.
解答:
解:设四个球的球心分别为O1、O2、O3、O4,将它们两两连结恰好组成一个正三棱锥,
且底面各棱长均为6,侧棱长均为4,
作O1H⊥面O2O3O4,垂足为H,则O1H为棱锥的高.
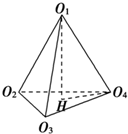
连接O4H,则O4H=
×6=2
,
∵O1H⊥面O2O3O4,
∴O1H⊥HO4,即∠O1HO4=90°,
∴O1H=
=2,
则从上面一个球的球心到桌面的距离为2+3=5,
故答案为:5
且底面各棱长均为6,侧棱长均为4,
作O1H⊥面O2O3O4,垂足为H,则O1H为棱锥的高.

连接O4H,则O4H=
| ||
| 3 |
| 3 |
∵O1H⊥面O2O3O4,
∴O1H⊥HO4,即∠O1HO4=90°,
∴O1H=
O1
|
则从上面一个球的球心到桌面的距离为2+3=5,
故答案为:5
点评:本题考查点到面的距离的计算,考查学生分析解决问题的能力,考查学生转化问题的能力,属于中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
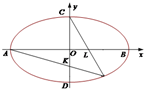 如图,设椭圆
如图,设椭圆