题目内容
已知函数f（x）=
sinωx+cos（ωx+
）+cos（ω-
）-1（ω＞0，x∈R），且函数f（x）的最小正周期为π．
（1）求函数f（x）的解析式并求f（x）的对称中心；
（2）在△ABC中，角A、B、C所对的边分别为a、b、c，若f（B）=1，S△ABC=
，且a+c=3+
，求边长b．
| 3 |
| π |
| 3 |
| π |
| 3 |
（1）求函数f（x）的解析式并求f（x）的对称中心；
（2）在△ABC中，角A、B、C所对的边分别为a、b、c，若f（B）=1，S△ABC=
3
| ||
| 4 |
| 3 |
考点：余弦定理,两角和与差的正弦函数,三角函数的周期性及其求法,正弦定理
专题：解三角形
分析：（1）利用三角函数的恒等变换化简函数的解析式为f（x）=2sin（ωx+
）-1，再根据周期性求得ω，从而求得它的对称中心．
（2）在△ABC中，由f（B）=1求得 B，根据S△ABC=
•ac•sinB，求得 ac，再利用a+c=3+
余弦定理可得b的值．
| π |
| 6 |
（2）在△ABC中，由f（B）=1求得 B，根据S△ABC=
| 1 |
| 2 |
| 3 |
解答：
解：（1）函数f（x）=
sinωx+cos（ωx+
）+cos（ω-
）-1=
sinωx-cosωx-1
=2sin（ωx+
）-1，
根据函数的周期为π=
，可得ω=2，故函数的解析式为f（x）=2sin（2x+
）-1；
令2x+
=kπ，k∈z，求得x=
-
，故函数的对称中心为（
-
，-1），k∈z．
（2）在△ABC中，∵f（B）=2sin（2B+
）=1，∴B=
．
∵S△ABC=
•ac•sinB=
，∴ac=3
．
再由a+c=3+
，利用余弦定理可得 b2=a2+c2-2ac•cosB=（a+c）2-2ac-
ac
=(3+
)2-2×3
-
×3
=3，
∴b=
．
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
=2sin（ωx+
| π |
| 6 |
根据函数的周期为π=
| 2π |
| ω |
| π |
| 6 |
令2x+
| π |
| 6 |
| kπ |
| 2 |
| π |
| 12 |
| kπ |
| 2 |
| π |
| 12 |
（2）在△ABC中，∵f（B）=2sin（2B+
| π |
| 6 |
| π |
| 6 |
∵S△ABC=
| 1 |
| 2 |
3
| ||
| 4 |
| 3 |
再由a+c=3+
| 3 |
| 3 |
=(3+
| 3 |
| 3 |
| 3 |
| 3 |
∴b=
| 3 |
点评：本题主要考查三角函数的恒等变换及化简求值，考查三角函数的周期性、对称性、余弦定理，属于中档题．．
练习册系列答案
相关题目
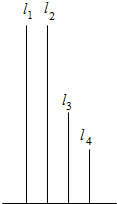
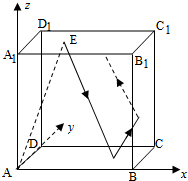如图，在长方体ABCD-A1B1C1D1中，AB=11，AD=7，AA1=12．一质点从顶点A射向点E（4，3，12），遇长方体的面反射（反射服从光的反射原理），将第i-1次到第i次反射点之间的线段记为li（i=2，3，4），l1=AE，将线段l1，l2，l3，l4竖直放置在同一水平线上，则大致的图形是（ ）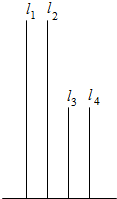
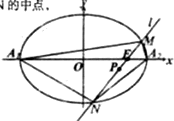已知椭圆C：
如图，已知椭圆E：