题目内容
1.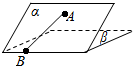 如图,二面角α-l-β的大小是30°,线段AB?α,B∈l,AB与l所成的角为30°.则AB与平面β所成的角的正弦值是$\frac{1}{4}$.
如图,二面角α-l-β的大小是30°,线段AB?α,B∈l,AB与l所成的角为30°.则AB与平面β所成的角的正弦值是$\frac{1}{4}$.
分析 过点A作平面β的垂线,垂足为C,在β内过C作l的垂线.垂足为D,连接AD,从而∠ADC为二面角α-l-β的平面角,连接CB,则∠ABC为AB与平面β所成的角,在直角三角形ABC中求出此角即可.
解答  解:过点A作平面β的垂线,垂足为C,
解:过点A作平面β的垂线,垂足为C,
在β内过C作l的垂线.垂足为D
连接AD,有三垂线定理可知AD⊥l,
故∠ADC为二面角α-l-β的平面角,为30°
又由已知,∠ABD=30°
连接CB,则∠ABC为AB与平面β所成的角
设AD=2,则AC=1,CD=$\sqrt{3}$,AB=4
∴sin∠ABC=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题主要考查了平面与平面之间的位置关系,以及直线与平面所成角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图为一个几何体的三视图
如图为一个几何体的三视图 如图,已知在直四棱柱ABCD-A1B1C1D1中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.
如图,已知在直四棱柱ABCD-A1B1C1D1中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.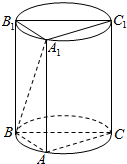 如图,四边形BCC1B1是圆柱的轴截面.AA1是圆柱的一条母线,已知AB=4,AC=2$\sqrt{2}$,AA1=3.
如图,四边形BCC1B1是圆柱的轴截面.AA1是圆柱的一条母线,已知AB=4,AC=2$\sqrt{2}$,AA1=3.