题目内容
设A、B两点在河的两岸,一测量者在A的同侧所在的河岸边选定一点C,测出AC的距离为50m,∠ACB=45°,∠CAB=105°后,算出A、B两点的距离为 m.
考点:余弦定理
专题:解三角形
分析:根据题意画出图形,如图所示,由∠ACB与∠CAB的度数求出∠ABC的度数,再由AC的长,利用正弦定理即可求出AB的长.
解答:
 解:在△ABC中,AC=50m,∠ACB=45°,∠CAB=105°,
解:在△ABC中,AC=50m,∠ACB=45°,∠CAB=105°,
∴∠ABC=30°,
由正弦定理
=
得:AB=
=
=50
(m),
故答案为:50
 解:在△ABC中,AC=50m,∠ACB=45°,∠CAB=105°,
解:在△ABC中,AC=50m,∠ACB=45°,∠CAB=105°,∴∠ABC=30°,
由正弦定理
| AC |
| sin∠ABC |
| AB |
| sin∠ACB |
| AC•sin∠ACB |
| sin∠ABC |
50×
| ||||
|
| 2 |
故答案为:50
| 2 |
点评:此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知B(-5,0),C(5,0)是△ABC的两个顶点,且sinB-sinC=
sinA,则顶点A的轨迹方程为( )
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
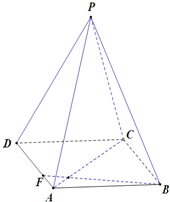 如图所示,正四棱锥P=ABCD中,AB=1,侧棱PA与底面ABCD所成角的正切值为
如图所示,正四棱锥P=ABCD中,AB=1,侧棱PA与底面ABCD所成角的正切值为