题目内容
设等差数列{an}的前n项和为Sn，若S6＞S7＞S5，则满足SkSk+1＜0的正整数k= ．
考点：等差数列的性质
专题：等差数列与等比数列
分析：解题首先由S6＞S7＞S5得到a6，a7的符号，进而推理出S12S13＜0得答案．
解答：
解：依题意a6=S6-S5＞0，a7=S7-S6＜0，则S11=
=11a6＞0，
S12=
=
＞0，S13=
=13a7＜0，
∴S12S13＜0，即满足SkSk+1＜0的正整数k=12．
故答案为：12．
| 11(a1+a11) |
| 2 |
S12=
| 12(a1+a12) |
| 2 |
| 12(a6+a7) |
| 2 |
| 13(a1+a13) |
| 2 |
∴S12S13＜0，即满足SkSk+1＜0的正整数k=12．
故答案为：12．
点评：本题考查数列的前n项和与通项an关系的应用，考查了等差数列的性质，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设l、m是两条不同的直线，α，β是两个不同的平面，则下列命题为真命题的是（ ）
| A、若m∥l，m∥α，则l∥α |
| B、若m⊥α，l⊥m，则l∥α |
| C、若α∥β，l⊥α，m∥β，则l⊥m |
| D、若m?α，m∥β，l?β，l∥α，则α∥β |
数列{an}是公差d不为零的等差数列，其前n项和为Sn，若记数据a1，a2，a3，…，a2015的方差为λ1，数据
，
，
，…，
的方差为λ2，则（ ）
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S2015 |
| 2015 |
| A、λ1＞λ2 |
| B、λ1=λ2 |
| C、λ1＜λ2 |
| D、与的大小关系与公差的正负有关 |
已知函数f（x）=ex-x2+8x，则在下列区间中f（x）必有零点的是（ ）
| A、（-2，-1） |
| B、（-1，0） |
| C、（0，1） |
| D、（1，2） |
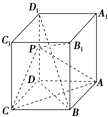如图，长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，点P为DD1的中点