题目内容
4.在数列{an}中,a1=1,${a_{n+1}}=2{a_n}+1(n∈{N^*})$,则数列$\left\{{\frac{1}{{1+{a_n}}}}\right\}$的各项和为2n-1.分析 由${a_{n+1}}=2{a_n}+1(n∈{N^*})$,变形an+1+1=2(an+1),利用等比数列的通项公式即可得出.
解答 解:∵${a_{n+1}}=2{a_n}+1(n∈{N^*})$,
∴an+1+1=2(an+1),
∴数列{an+1}是等比数列,首项为2,公比为2.
∴an+1=2n,
∴an=2n-1.
故答案为:2n-1.
点评 本题考查了等比数列的通项公式,考查了变形能力与计算能力,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
13.已知集合A={2,3,4},B={2,4,6},则A∩B=( )
| A. | {2} | B. | {2,4} | C. | {2,4,6} | D. | {2,3,4,6} |
15.若执行如图所示的程序框图后,输出的结果是-29,则判断框中的整数k的值是( )
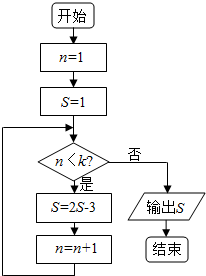

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
12.若直线l过点(3,2)与双曲线4x2-9y2=36只有一个公共点,则这样的直线有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
13.焦点在x轴,且焦点到准线的距离为4的抛物线方程为( )
| A. | y2=4x | B. | y2=8x | C. | y2=±4x | D. | y2=±8x |
14.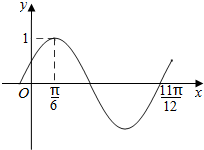 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )| A. | $\frac{π}{24}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |