题目内容
4.设P是一个数集,且至少含有两个数,若对任意a,b∈P,都有a+b,a-b,ab,$\frac{a}{b}$∈P(除数b≠0),则称P是一个数域.例如有理数集Q是数域.求证:(1)数域必含有0与1两个数;
(2)数域必为无限集;
(3)数集A={x|x=a+b•$\sqrt{2}$,a,b∈Q}是数域.
分析 ①根据特例a-a=0,$\frac{a}{a}$=1,可得证;
②特例一定有1+1=2,1+2=3,推下去必然包含整数集,故得证;
③根据数域的定义证明对加,减,乘,除封闭即可.
解答 证明:①数集P有两个元素a,b,则一定有a-a=0,$\frac{a}{a}$=1,故数域必含有0与1两个数,故(1)得证;
(2)数域有1,一定有1+1=2,1+2=3,推下去必然包含整数集,因而为无限集,(2)得证;
(3)当b=0是,数集A=Q,当b≠0时,数集A表示所有含$\sqrt{2}$的同类二次根式,可知,从A中任取m,n,都有其和,差,积,商仍然在集合A中,根据定义可得数集A为数域即复数集.
点评 对新型定义的考查,应紧扣定义,从定义入手.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.$\overrightarrow{a}•\overrightarrow{b}$=-8,|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=4$\sqrt{2}$,则<$\overrightarrow{a}$,$\overrightarrow{b}$>是( )
| A. | 0° | B. | 90° | C. | 180° | D. | 270° |
16.直线xcosα-y+sinα=0,则该直线倾斜角的取值范围是( )
| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,$\frac{3π}{4}$] | C. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |
13.$\frac{2-3i}{3+2i}$等于( )
| A. | -$\frac{1}{5}$i | B. | $\frac{1}{5}$i | C. | -i | D. | i |
11.已知直线l:y=kx+b,曲线C:x2+y2-2x=0,则“k+b=0”是“直线l与曲线C有公共点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
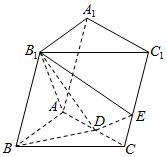 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.