题目内容
11.已知直线l:y=kx+b,曲线C:x2+y2-2x=0,则“k+b=0”是“直线l与曲线C有公共点”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 联立方程组,得到(1+k2)x2+(2kb-2)x+b2=0,根据△=(2kb-2)2-4(1+k2)b2≥0,得到b(k+b)-1≤0,结合充分必要条件判断即可.
解答 解:由直线l:y=kx+b,曲线C:x2+y2-2x=0,
得:$\left\{\begin{array}{l}{y=kx+b}\\{{x}^{2}{+y}^{2}-2x=0}\end{array}\right.$,
∴(1+k2)x2+(2kb-2)x+b2=0,
若直线和曲线有公共点,
则△=(2kb-2)2-4(1+k2)b2≥0,
∴b(k+b)-1≤0,
则“k+b=0”是“直线l与曲线C有公共点”的充分不必要条件,
故选:A.
点评 本题考查了充分必要条件,考查直线和曲线的交点问题,是一道基础题.

练习册系列答案
相关题目
2.设Sn是等差数列{an}的前n项和,若$\frac{{S}_{3}}{{S}_{6}}$=$\frac{1}{4}$,则$\frac{{S}_{6}}{{S}_{12}}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
16.若指数函数y=(2a-1)x在R上为单调递减函数,则a的取值范围是( )
| A. | (0,1) | B. | ($\frac{1}{2}$,+∞) | C. | ($\frac{1}{2}$,+1) | D. | (1,+∞) |
3.设实数x,y满足$\left\{\begin{array}{l}{y≤2x+2}\\{x+y-3≥0}\\{x≤2}\end{array}\right.$,则$\frac{y}{x}$的取值范围是( )
| A. | [$\frac{1}{2}$,8] | B. | [$\frac{1}{2}$,3] | C. | [3,8] | D. | [$\frac{1}{2}$,+∞) |
20.执行如图的程序框图,若t输入(a,a+1)中的数值,输出的S是单调增加的,则实数a的取值范围是( )
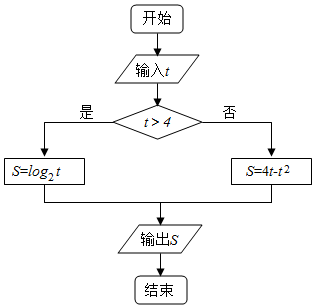

| A. | (-∞,1) | B. | [1,4] | C. | (-∞,1]∪(4,+∞) | D. | (-∞,1]∪[4,+∞) |