题目内容
已知直线l：5ax-5y-a+3=0．
（1）证明：不论a为何值，直线l总经过第一象限；
（2）若直线l不经过第二象限，求a的范围．
（1）证明：不论a为何值，直线l总经过第一象限；
（2）若直线l不经过第二象限，求a的范围．
考点：直线的一般式方程
专题：数形结合,直线与圆
分析：（1）只需证明不论a为何值，直线l总过第一象限的点即可；
（2）根据题意，画出图形，结合图形，即可求出直线l不经过第二象限时a的取值范围．
（2）根据题意，画出图形，结合图形，即可求出直线l不经过第二象限时a的取值范围．
解答：
解：（1）证明：∵直线l为5ax-5y-a+3=0，
即a（5x-1）+（-5y+3）=0；
∴
，
解得
；
∴不论a为何值，直线l总过第一象限的点（
，
），
即直线l过第一象限；
（2）根据题意，画出图形，如图所示，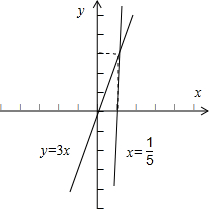
；
∵直线l不经过第二象限，∴-a+3≤0，即a≥3；
l的斜率a满足a≥3；
∴a的取值范围是{a|a≥3}．
即a（5x-1）+（-5y+3）=0；
∴
|
解得
|
∴不论a为何值，直线l总过第一象限的点（
| 1 |
| 5 |
| 3 |
| 5 |
即直线l过第一象限；
（2）根据题意，画出图形，如图所示，
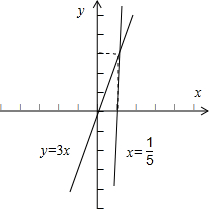；∵直线l不经过第二象限，∴-a+3≤0，即a≥3；
l的斜率a满足a≥3；
∴a的取值范围是{a|a≥3}．
点评：本题考查了直线方程的应用问题，解题时应用直线恒过定点的问题，数形结合思想求直线的斜率取值范围等知识，是基础题．
练习册系列答案
相关题目