题目内容
6.已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=$\frac{1}{2}$(|x-a|+|x-2a|-3|a|).若集合{x|f(x-1)-f(x)>0,x∈R}=∅,则实数a的取值范围为$(-∞,\frac{1}{6}]$.分析 把x≥0时的f(x)改写成分段函数,求出其最小值,由函数的奇偶性可得x<0时的函数的最大值,条件等价为对?x∈R,都有f(x-1)≤f(x),进行转化求解即可求解该不等式得答案.
解答 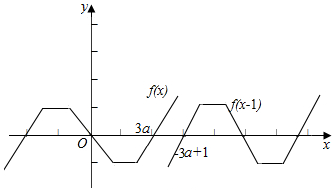 解:若{x|f(x-1)-f(x)>0,x∈R}=∅,
解:若{x|f(x-1)-f(x)>0,x∈R}=∅,
则等价为f(x-1)-f(x)≤0恒成立,即f(x-1)≤f(x)恒成立,
当x≥0时,f(x)=$\frac{1}{2}$(|x-a|+|x-2a|-3|a|).
若a≤0,则当x≥0时,f(x)=$\frac{1}{2}$(x-a+x-2a+3a)=x,
∵f(x)是奇函数,
∴若x<0,则-x>0,则f(-x)=-x=-f(x),
则f(x)=x,x<0,
综上f(x)=x,此时函数为增函数,则f(x-1)≤f(x)恒成立,
若a>0,
若0≤x≤a时,f(x)=$\frac{1}{2}$[-x+a-(x-2a)-3a]=-x;
当a<x≤2a时,f(x)=$\frac{1}{2}$[x-a-(x-2a)-3a]=-a;
当x>2a时,f(x)=$\frac{1}{2}$(x-a+x-2a-3a)=x-3a.
即当x≥0时,函数的最小值为-a,
由于函数f(x)是定义在R上的奇函数,
当x<0时,f(x)的最大值为a,
作出函数的图象如图:
由于?x∈R,f(x-1)≤f(x),
故函数f(x-1)的图象不能在函数f(x)的图象的上方,
结合图可得1-3a≥3a,即6a≤1,求得0<a≤$\frac{1}{6}$,
综上a≤$\frac{1}{6}$,
故答案为:(-∞,$\frac{1}{6}$]
点评 本题主要考查带有绝对值的函数,奇函数的性质,函数的图象特征,根据分段函数的性质,将条件转化不等式恒成立是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
16.设函数f(x)=x3-ax2+2bx+1的导函数为f′(x),若函数f′(x)的图象关于直线x=$\frac{2}{3}$对称,且当x∈[1,π]时,恒有f(x)≥1,则实数b的取值范围为( )
| A. | ($\frac{1}{2}$,+∞) | B. | [$\frac{1}{2}$,1] | C. | (-∞,$\frac{1}{2}$] | D. | [$\frac{1}{2}$,+∞) |
14.与命题“|x|”=“|y|”等价的命题是( )
| A. | x=y | B. | x3=y3 | C. | x2=y2 | D. | $\sqrt{x}$=$\sqrt{y}$ |
11.在空间直角坐标系中,在x轴上的点P(m,0,0)到点P1(4,1,2)的距离为$\sqrt{30}$,则m的值为( )
| A. | -9或1 | B. | 9或-1 | C. | 5或-5 | D. | 2或3 |