题目内容
16.若x${\;}^{\frac{1}{2}}$-x${\;}^{-\frac{1}{2}}$=3,则x+x-1=( )| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
分析 把已知等式两边平方即可求得答案.
解答 解:由x${\;}^{\frac{1}{2}}$-x${\;}^{-\frac{1}{2}}$=3,
两边平方得:$({x}^{\frac{1}{2}}-{x}^{-\frac{1}{2}})^{2}=9$,
即x+x-1-2=9,
∴x+x-1=11.
故选:C.
点评 本题考查根式与分数指数幂的互化及运算,能够想到把已知等式两边平方是关键,是基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
4.下列有关命题的说法中正确的是( )
| A. | 若命题“p∧q”为假,则“p∨q”也为假 | |
| B. | 命题“?x0∈R,x${\;}_{0}^{2}$+x0+1<0”的否定是“?x∈R,x2+x+1<0” | |
| C. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
8.在正三棱柱ABC-A1B1C1中,若AB1⊥BC1,则下列关于直线A1C和AB1,BC1的关系的判断正确的为( )
| A. | A1C和AB1,BC1都垂直 | B. | A1C和AB1垂直,和BC1不垂直 | ||
| C. | A1C和AB1,BC1都不垂直 | D. | A1C和AB1不垂直,和BC1垂直 |
5.已知命题p:关于x的函数y=x2-3ax+4在[1,+∞)上是增函数,命题q:函数y=(2a-1)x为减函数,若“p且q”为假命题,则实数a的取值范围是( )
| A. | (-∞,$\frac{1}{2}$]∪($\frac{2}{3}$,+∞) | B. | (-∞,$\frac{1}{2}$] | C. | ($\frac{2}{3}$,+∞) | D. | ($\frac{1}{2}$,$\frac{2}{3}$] |
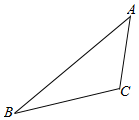 在△ABC中,AC=$\sqrt{2}$,AB=$\sqrt{3}$+1,∠BAC=45°,点P满足:$\overrightarrow{BP}$=(1-λ)$\overrightarrow{BA}$+λ$\overrightarrow{BC}$(λ>0),AP=$\frac{\sqrt{2}}{2}$.
在△ABC中,AC=$\sqrt{2}$,AB=$\sqrt{3}$+1,∠BAC=45°,点P满足:$\overrightarrow{BP}$=(1-λ)$\overrightarrow{BA}$+λ$\overrightarrow{BC}$(λ>0),AP=$\frac{\sqrt{2}}{2}$.